Oblique collision of two bodies undergoing projectile motion

[Sujith Sizon]

Q) two identical smooth balls are projected from points O and A on the horizontal ground with the same speed of projection the angle of projection in each case is 30 The distance between O and A is 100m . The balls collide in mid air And return to their respective points of projection if coefficient of restitution is 0.7 find the speed of projection of either ball (m/s) correct to nearest integer ?

Question figure

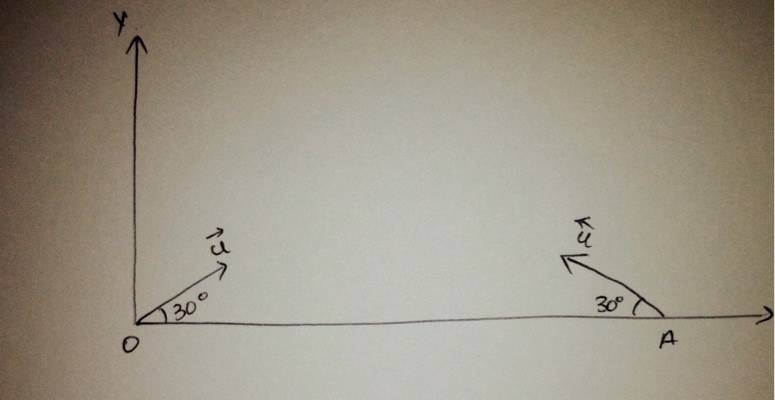
My Attempt :

Taking $y$ as the height from the ground to the point where the masses collide and $\alpha$ as the angle made by the final velocity vector with the horizontal .

Using projectile equation ie : $y=x\tan\theta\left[1-\frac{x}{R}\right]$

For the case when it is projected and reaches a height $y$

$y=\frac{50}{\sqrt{3}}\left[1-\frac{50\times 20}{\sqrt{3}u^{2}}\right]$

For its return path considering a projectile motion from height $y$ with velocity vector making an angle $\alpha$ with the horizontal we get

$y=50\tan\alpha\left[1-\frac{50\times g}{v^{2}\sin2\alpha}\right]$

The from coefficient of restitution formula we get

$e\rightarrow0.7=\frac{2v\cos\alpha}{2u\cos30}$

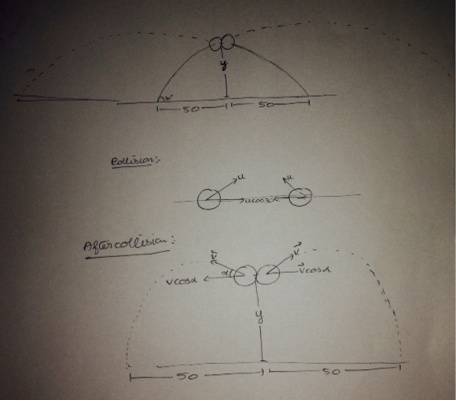
Now assuming that my procedure so far is appropriate i need one more equation so that i can find $u$ and $v$

SOLVED (thanks to TSny)

Conserving momentum along tangential component we will have
$2mu\sin30 = 2mv\sin\alpha$

 

[TSny]

Welcome to PF!

What happens to the vertical component of velocity of each smooth ball during the collision?

 

[Sujith Sizon]

Welcome to PF!

What happens to the vertical component of velocity of each smooth ball during the collision?

It changes but we can't conserve momentum along vertical because of gravitational force acting, right ?

 

[TSny]

You can forget about the effect of gravity during the very small time interval of the collision. The only important forces during the collision are the large contact forces between the two balls. (This is sometimes called the "impulse approximation" for collisions.)

 

[Sujith Sizon]

You can forget about the effect of gravity during the very small time interval of the collision. The only important forces during the collision are the large contact forces between the two balls. (This is sometimes called the "impulse approximation" for collisions.)

Which Impulse force ? the velocity changes only due to collision right ?

 

[TSny]

Yes. To a good approximation, the only force that causes a change in velocity of one of the balls during the collision is the impulsive contact force from the other ball.

 

[Sujith Sizon]

Yes. To a good approximation, the only force that causes a change in velocity of one of the balls during the collision is the impulsive contact force from the other ball.

Okay so this impulse contact force will be along horizontal right (along the surface of contact) , then we will have to find its value( of Impulse contact force) also , how will we find that ?

Im guessing J= Change in momentum along horizontal,
$J=mu\cos30 - mv\cos\alpha$

 

[TSny]

Yes, for smooth surfaces the contact force will be horizontal (perpendicular to the surfaces of the balls at the point of contact). You do not need to determine the contact force; the coefficient of restitution gives you everything you need to know about the effect of the contact force on the horizontal components of velocity of the balls. You have already taken care of this in your equations. But, you have not yet used important information that you can deduce about the vertical components of velocity.

 

[Sujith Sizon]

Yes, for smooth surfaces the contact force will be horizontal (perpendicular to the surfaces of the balls at the point of contact). You do not need to determine the contact force; the coefficient of restitution gives you everything you need to know about the effect of the contact force on the horizontal components of velocity of the balls. You have already taken care of this in your equations. But, you have not yet used important information that you can deduce about the vertical components of velocity.

So you are asking me to conserve momentum along vertical as
$2mu\sin30 = 2mv\sin\alpha$
But then it will mean that there is no change in its vertical component of velocity , but there should be right , only the would it be able to reach back to its initial position right ?

 

[Sujith Sizon]

So you are asking me to conserve momentum along vertical as
$2mu\sin30 = 2mv\sin\alpha$
But then it will mean that there is no change in its vertical component of velocity , but there should be right , only the would it be able to reach back to its initial position
Is my third figure apt ?

 

[TSny]

So you are asking me to conserve momentum along vertical as
$2mu\sin30 = 2mv\sin\alpha$
But then it will mean that there is no change in its vertical component of velocity , ...

Yes, that's right. Without a vertical component of force, the balls do not change their vertical component of velocity during the collision.

...but there should be right , only the would it be able to reach back to its initial position right ?

I'm not sure why you believe this.

 

[TSny]

Your third figure looks good to me.

 

[Sujith Sizon]

Yes, that's right. Without a vertical component of force, the balls do not change their vertical component of velocity during the collision.

oh okay because coefficient of restitution which is amount of change in speed only along impact axis so along tangential component it ought not to change and because of impulse approximations we are neglecting gravitational force , well then i will have my equation , thanks for your time .

 

[TSny]

OK, sounds good.