Obtaining potential from Lorentz Force

[iScience]

Two part inquiry


PART I


Situation: I have a B-field and I'm pulling a straight piece of wire through that B-field

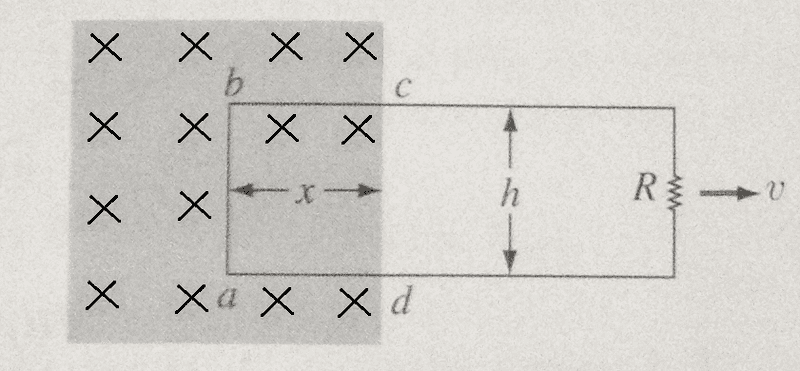
You pull the wire perpendicularly through the B-field at velocity v; charges between points a and b will experience the Lorentz Force and will begin to move along the wire with velocity u, and thus will experience a force opposite to the direction which you are pulling the wire.



Goal: Trying to derive the work done on a unit charge the classical way (by integrating along the path it takes)


Let us define the force per unit q to pull the wire through the field: f(pull)$\equiv$uB


$$\int f_{pull} \cdot dl = (uB) \frac{y}{cosθ}sinθ= vBhy$$



Problem: The vector f(pull) should be pointing outward (opposite the direction of wire pulling). so then shouldn't there be a negative sign somewhere?

--------------------


PART II


I decided to try and derive it my own way and i ran into a problem somewhere but i can't seem to spot where it is.


I said that, there is a vertical work component and a horizontal work component.

vertical work component

(From the initial pull)

$$W_y= \int (q\vec{v} \times \vec{B}) \cdot dy = (qvB)y= qvBy$$


horizontal work component

$$W_x= \int (q\vec{u} \times \vec{B}) \cdot dx = quBx =quBytanθ$$


vectorial sum

(yes i know work is a scalar quantity. but there is a work in x direction and work in the y direction so i thought i'd try this approach)

$$W= \sqrt{(qvBy)^2+(quBytanθ)2}= qBy\sqrt{v^2+u^2tan^2θ}$$

but since utanθ=v

$$W=qBy\sqrt{2v^2}=\sqrt{2}qvBy$$

i'm off by a factor of $\sqrt{2}$


Could someone please help me find the mistake in doing it this way?


help is much appreciated. ty all!

 

[rude man]

You are an observer at rest with the B field, watching the wire move by to the right.

There are 4 forces involved:
1. Lorentz force on the unit charge due to the wire motion in the x direction.
2. Lorentz force due to the motion of the charge in the y direction.
3. Since the force in 2 doesn't pull the charge out of the wire in the -x direction there must be a third force keeping the charge in the wire.
4. There is also a force along the wire associated with the collision of the electrons as they move up the wire.
This force obviously represents work since it's heating up the wire.

You need to analyze these four forces, determine which ones contribute to work done on the unit charge as it moves thru the wire and around the rest of the closed loop. Remember that the B field does no work on any charge. So, hint: think about the last two forces!