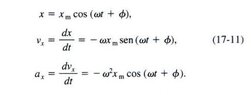Student084
- 4
- 0
- Homework Statement
- Omission of parts of equations in solving oscillation questions.
- Relevant Equations
- a(t)=W² Xm cos(wt+ϕ)
x(t)= Xm e^(-bt/2m) cos(w't+ϕ)
Perhaps that's a very dumb question, but I'm having a hard time to understand why it's possible to omit parts of the equations in solving various problems involving oscillations. Here, for example, the complete equation for acceleration is not used (the part with cosine doesn't appear) and here the complete equation for displacement in damped oscillations (the part with cosine doesn't appear) is also not used.