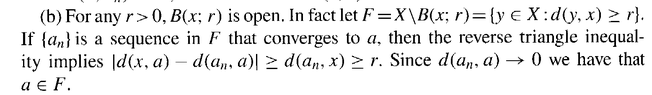Open and Closed Sets .... Conway, Example 5.3.4 (b) .... ....

[Math Amateur]

I am reading John B. Conway's book: A First Course in Analysis and am focused on Chapter 5: Metric and Euclidean Spaces ... and in particular I am focused on Section 5.3: Open and Closed Sets ...

Conway's Example 5.3,4 (b) reads as follows ... ... View attachment 8938Note that Conway defines open and closed sets as follows:View attachment 8939Now ... in the text of Example 5.3.4 shown above we read the following:

" ... ... the Reverse Triangle Inequality implies $$\mid d(x,a) - d( a_n, a ) \mid \ge d(a_n, x) \ge r$$ ... ... "Can someone please explain to me exactly why $$\mid d(x,a) - d( a_n, a ) \mid \ge d(a_n, x) \ge r$$ ...

My thoughts on this are as follows ...

It seems to me that the Reverse Triangle Inequality implies $$\mid d(x,a) - d( a_n, a ) \mid \le d(a_n, x)$$ ... ?Hope someone can clarify the above issue ...

Peter===================================================================================The above post mentions the Reverse Triangle Inequality ... Conway's statement of that inequality is as follows:View attachment 8940Hope that helps ..

Peter

 

[Ackbach]

Conway's statement of the Reverse Triangle Inequality is correct, so I agree with you that it is puzzling how Conway could possibly be using the Reverse Triangle Inequality correctly in the proof. In fact, you can draw yourself a picture as a counter-example to the specific claim you mentioned. Imagine the $\{a_n\}$ sequence is moving out from $x$ towards $a$, but not on the straight line from $x$ to $a$ (and here, just to keep things simple, use the 2D euclidean space). Then the claim that $|d(x,a)-d(a_n,a)|\ge d(a_n,x)$ is false.

I think what Conway is trying to prove is still correct, but it can't be proved that way. Here is an alternative candidate proof (not guaranteed to be correct at all, but maybe it moves in the right direction).

Claim: for any $r>0, B(x; r)$ is open.

Proof: Let $r>0$ and $F=X\setminus B(x;r)=\{y\in X: d(y,x)\ge r\}.$ Let $\{a_n\}\in F$ converge to $a.$ By definition of convergence, $d(a_n,a)\to 0.$ We want to show that $d(x,a)\ge r.$ Suppose, by way of contradiction, that $d(x,a)<r.$ Then there exists $\varepsilon>0$ such that $d(x,a)+\varepsilon<r$ (say, $\varepsilon=(r-d(x,a))/2.$) Now consider the ball $B(a;\varepsilon).$ The idea here is that the $a_n$'s are going to have to get inside that ball, which is not allowed to happen on account of where the $a_n$'s live. Details: because $a_n\to a,$ there exists $N>0$ such that if $n>N,\; d(a_n,a)<\varepsilon.$ But by the Triangle Inequality, $n>N$ implies
$$d(x,a_n)\le d(x,a)+d(a,a_n)< d(x,a)+\varepsilon<r,$$
contradicting that $a_n\in F.$ Therefore, $a\in F,$ making $F$ closed and $B(x;r)$ open.

How does that strike you?

 

[Math Amateur]

Conway's statement of the Reverse Triangle Inequality is correct, so I agree with you that it is puzzling how Conway could possibly be using the Reverse Triangle Inequality correctly in the proof. In fact, you can draw yourself a picture as a counter-example to the specific claim you mentioned. Imagine the $\{a_n\}$ sequence is moving out from $x$ towards $a$, but not on the straight line from $x$ to $a$ (and here, just to keep things simple, use the 2D euclidean space). Then the claim that $|d(x,a)-d(a_n,a)|\ge d(a_n,x)$ is false.

I think what Conway is trying to prove is still correct, but it can't be proved that way. Here is an alternative candidate proof (not guaranteed to be correct at all, but maybe it moves in the right direction).

Claim: for any $r>0, B(x; r)$ is open.

Proof: Let $r>0$ and $F=X\setminus B(x;r)=\{y\in X: d(y,x)\ge r\}.$ Let $\{a_n\}\in F$ converge to $a.$ By definition of convergence, $d(a_n,a)\to 0.$ We want to show that $d(x,a)\ge r.$ Suppose, by way of contradiction, that $d(x,a)<r.$ Then there exists $\varepsilon>0$ such that $d(x,a)+\varepsilon<r$ (say, $\varepsilon=(r-d(x,a))/2.$) Now consider the ball $B(a;\varepsilon).$ The idea here is that the $a_n$'s are going to have to get inside that ball, which is not allowed to happen on account of where the $a_n$'s live. Details: because $a_n\to a,$ there exists $N>0$ such that if $n>N,\; d(a_n,a)<\varepsilon.$ But by the Triangle Inequality, $n>N$ implies
$$d(x,a_n)\le d(x,a)+d(a,a_n)< d(x,a)+\varepsilon<r,$$
contradicting that $a_n\in F.$ Therefore, $a\in F,$ making $F$ closed and $B(x;r)$ open.

How does that strike you?

Your proof looks good to me, Ackbach ...

Thanks for your help on this issue ...

Peter

 

[Ackbach]

Your proof looks good to me, Ackbach ...

Thanks for your help on this issue ...

Peter

You're very welcome! It was a fun problem.

 

[Ackbach]

Update from Dr. Conway:

Your student is correct and I am not sure why I was trying to work in the reverse triangle inequality. The correct argument is as follows. Using the notation in the book we note that $$r \le d(a_n, x) \le d(a_n, a) + d(a, x) \to d(a, x).$$

 

[Opalg]

Update from Dr. Conway:

Your student is correct and I am not sure why I was trying to work in the reverse triangle inequality. The correct argument is as follows. Using the notation in the book we note that $$r \le d(a_n, x) \le d(a_n, a) + d(a, x) \to d(a, x).$$

Peter should get a special award for the number of errors he has found in textbooks!