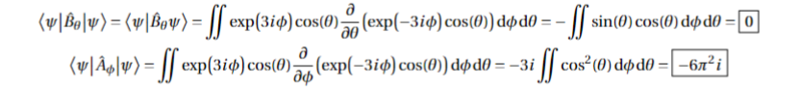Operators On Multivariable Wave Functions

[flyusx]

Homework Statement

Are $\hat{A}=\frac{\partial}{\partial\phi}$ and $\hat{B}=\frac{\partial}{\partial\theta}$ Hermitian? Given $\psi(\theta,\phi)=\exp(-3i\phi)\cos(\theta)$, evaluate <ψ|Α|ψ>, <ψ|Β|ψ>

Relevant Equations

Hermitian functions can act either on the bra or ket first; non-Hermitian functions do not have tis ability. <φ|ψ>$=\int\phi^{*}\psi$

I know the way to solve the first part is to find <ψ|Αψ> and compare it with <ψΑ|ψ>. This comparison can be done through an integral representation where we take ψ* and act A on ψ to be the integrand, or act A on ψ* and multiply by ψ for the integrand. If the integrals are the same, then the operator is Hermitian. (Another way is to check the eigenvalues and see if they are purely real). My question is: after computing the integrand, do we expand the integral out as a double integral with respect to dφdθ? Or do we only expand it in terms of dθ since the exponential term cancels out? I assume the bounds for the integral will be from 0 to 2π as this would represent a full 'declination and ascension' over space. Knowing this will help me solve both parts.

If it's of any use, this is Exercise 2.52 of Zettili's Quantum Mechanics. I referred to his solved Problem 2.19 to see the best way to represent an inner product, but the wave functions there were solely dependent on x and thus integrated with respect to dx. I couldn't find an example where an inner product of a multivariable wave function was expanded out in integral form.

 

[DrClaude]

My guess is that you have to work in both $\theta$ and $\phi$, and integrate with the proper integration element, $\sin \theta \, d\theta \, d \phi$.

 

[flyusx]

I thought $$\langleψ(x)|\hat{A}|ψ(x)\rangle$$ meant $$\int\psi^{*}\hat{A}\psi\;dx$$, and ended up figuring out that one does integrate over all elements (for instance, x,y,z or in this case θ,φ). I know that in spherical coordinates, volume integration isn't simply dρdθdφ, but I thought that an expectation value calculation was defined to be $\int\psi^{*}\hat{A}\psi\;dx$ over all space.

Either way, I've linked a photo of my solution. The integral was evaluated from 0 to 2π.

 

[DrClaude]

I thought $$\langleψ(x)|\hat{A}|ψ(x)\rangle$$ meant $$\int\psi^{*}\hat{A}\psi\;dx$$,

$\ket{\psi(x)}$ doesn't make sense. $\ket{\psi}$ is an (abstract) vector in Hilbert space, so it doesn't make sense to write it as having a position dependence. To convert to a wave function, you have
$$
\psi(x) = \braket{x | \psi}
$$

but I thought that an expectation value calculation was defined to be $\int\psi^{*}\hat{A}\psi\;dx$ over all space.

If you have, for example, a particle on a ring, "all space" means "anywhere on the ring", which can be parametrized by a single angle $\theta$.

Either way, I've linked a photo of my solution. The integral was evaluated from 0 to 2π.

I don't see the $\sin \theta$ in the integration element. Also, you are not showing anything here about hermiticity.

 

[flyusx]

A is anti-Hermitian, B is Hermitian. I'd figured that part by myself so I didn't bother to link it. Sorry.

Does $\sin(θ)$ come from spherical integration? I've seen $ρ^2\sin(θ)$ for a volume integral but I can't conceptualise where the sine comes from.

 

[DrClaude]

Does $\sin(θ)$ come from spherical integration? I've seen $ρ^2\sin(θ)$ for a volume integral but I can't conceptualise where the sine comes from.

https://en.wikipedia.org/wiki/Spher..._and_differentiation_in_spherical_coordinates

 

[flyusx]

Thanks, I checked out the section/page about solid angle. But <ψ|Α|ψ> would be zero as $$\int_{0}^{2\pi}\int_{0}^{2\pi}\sin(\theta)\cos^{2}(\theta)\;d\theta d\phi=0$$. <ψ|Β|ψ> would also remain zero. Is this reasonable, or are my integral bounds wrong?

 

[PeroK]

are my integral bounds wrong?

The polar angle $\theta$ runs from $0$ to $\pi$.

 

[flyusx]

Yes, I am blind. Thank you.