SUMMARY
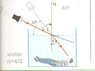
The actual angle of refraction from the surface of the water is 37 degrees, derived from the relationship defined by Snell's Law, which states that n1 * sin(i) = n2 * sin(r). In this case, the apparent angle of incidence (i) is 53 degrees, leading to the conclusion that the angle of refraction (r) is calculated as 90 - 53 = 37 degrees. This relationship highlights the geometric principles involved in light behavior at the water-air interface.
PREREQUISITES
- Understanding of Snell's Law in optics
- Basic geometry concepts related to angles
- Familiarity with the concept of refraction
- Knowledge of light behavior at different mediums
NEXT STEPS
- Study the derivation and applications of Snell's Law in various mediums
- Explore the geometric interpretation of angles in optics
- Investigate the principles of total internal reflection
- Learn about the refractive indices of common materials, including water and air
USEFUL FOR
Students studying physics, particularly those focusing on optics, as well as educators seeking to clarify concepts of refraction and angle relationships in light behavior.