Optimal time for scheduling the tasks

[mathmari]

Hey!

We have the following tasks with the respective times of execution:
\begin{equation*}\begin{matrix}T_1/5 & T_2/4 & T_3/8 & T_4/3 & T_5/4 & T_6/6 & T_7/8 & T_8/3 & T_9/5 & T_{10}/3\end{matrix}\end{equation*} The tasks $T_3,T_4$ have as prerequisite the task $T_2$, the tasks $T_5, T_6, T_7$ have as prerequisite the task $T_4$ and the tasks $T_8, T_9$ have as prerequisite the task $T_7$. Make the schedule of these tasks using three processors so that the time of execution of the tasks $\omega$ is not more than $5/3$ of the optimal time for the execution of the tasks.


First I made a diagramm of the tasks in respect of the prerequisites:

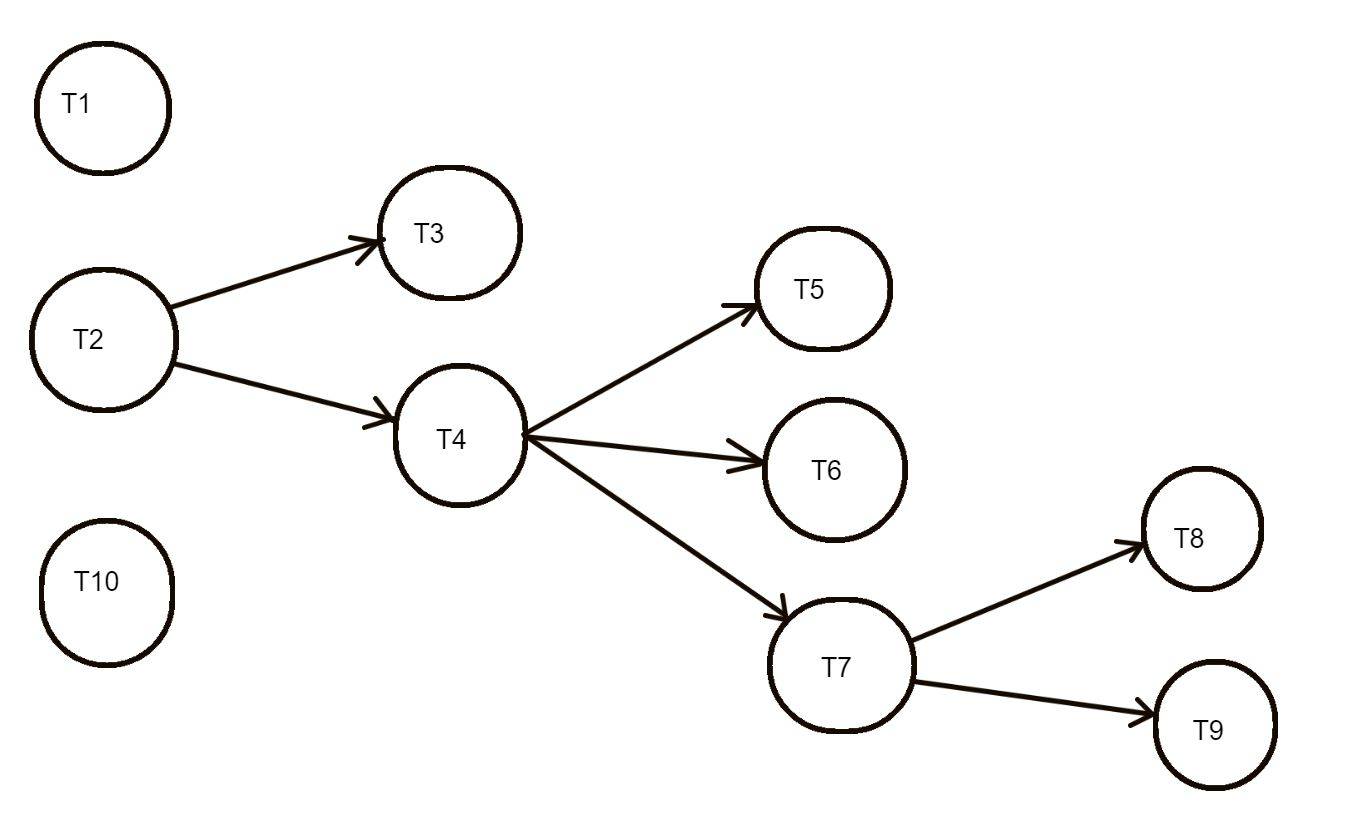Then using 3 processors I got the following:

Is this correct? This means that the time needed for the execution of the tasks is $\omega=20$, right?

But which is the optimal time for the execution of the tasks, since $\omega$ has to less or equal to $5/3$ of that optimal time?

Or is the way I did the above wrong?


:unsure:

 

[I like Serena]

This means that the time needed for the execution of the tasks is $\omega=20$, right?

Hey mathmari!

Looks correct to me. (Nod)

But which is the optimal time for the execution of the tasks, since $\omega$ has to less or equal to $5/3$ of that optimal time?

That depends on how the 'optimal time for the execution of the tasks' is defined.
Is that somewhere in your texts? I can't seem to easily find it. (Wondering)

If I had to guess given the context, I'd guess that it is the time needed if all CPU's run at 100% without wasting any time waiting.
Alternatively it might be the time needed if we had an infinite number of processors.