- #1
- 18,994
- 23,995
Questions
1.) (disclosed by @Demystifier ) Using the notion of double integrals prove that $$B(m,n) = \frac{\Gamma (m) \Gamma (n)}{\Gamma (m + n)}\; \;(m \gt 0\,,\, n\gt 0)$$ where ##B## and ##\Gamma## are the Beta and Gamma functions respectively.
2.) (solved by @Math_QED ) Show that the Fourier series of an even function cannot contain sine.
3.) (solved by @Bosko ) Show that $$\int_{0}^{1} dx \int_{x}^{\sqrt{x}} f(x,y)\,dy = \int_{0}^{1} dy \int_{y^2}^{y} f(x,y)\,dx\,.$$
4.) The graphic of eye colors shows us the probability of baby's eye color in dependency of the parents'. This yields the following multiplication table:
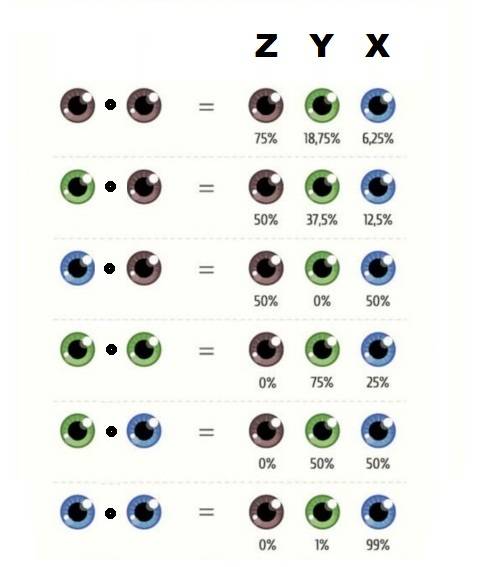
\begin{align*}
x \cdot x &= (3/4) x + (3/16) y + (1/16) z\\
x \cdot y &=(1/2) x+(3/8) y+(1/8) z\\
x \cdot z &=(1/2) x+(1/2) z\\
y \cdot y &=(3/4) y+(1/4) z\\
y \cdot z &=(1/2) y+(1/2) z\\
z \cdot z &= z
\end{align*}
which we extend to a real, commutative, distributive, three dimensional algebra ##A##.
a) (solved by @fbs7 ) Is ##A## an associative algebra?
still open:
b) Prove, that ##A## is a baric algebra, i.e. show that there is a non trivial algebra homomorphismus ##\omega\, : \,A\longrightarrow \mathbb{R}##, the weight function.
c) Determine a basis for ##\operatorname{ker}\omega## and rewrite the multiplication table according to this new basis.
d) Prove that there is an ideal ##N## of codimension one in ##A##, such that ##A^2 \nsubseteq N##.
e) A algebra is called genetic, if there is a basis ##\{\,u_i\,\}## such that the structure constants ##\lambda_{ijk}## defined by
$$
u_i \cdot u_j = \sum_{k=1}^n \lambda_{ijk}u_k
$$
fulfill the following conditions:
f) Show that ##A## is not a genetic algebra.
g) Determine all idempotent elements of ##A##. Is there a basis of ##A## with idempotent elements?
5.) (solved by @Bosko ) Prove that starting with ##\frac{1}{1}## the following binary tree
$$
\begin{array}{ccccc}
&&\frac{a}{b}&&\\
&\swarrow &&\searrow \\
\frac{a}{a+b}&&&&\frac{a+b}{b}
\end{array}
$$
defines a counting of all positive rational numbers without repetition and all quotients canceled out.
6.) (solved by @Cthugha ) Who said what here? (What is the task, who a bonus.)

7.) (solved by @lpetrich ) Calculate ##I:=\int_0^\infty \dfrac{\sqrt{x^{e-2}}}{x^e+1}\,dx##
8.) An algebra ##A## is a vector space with a binary distributive multiplication. An example are group algebras, i.e. the distributive extension of the formal basis vectors ##g\in G## such as $$A :=\mathbb{R}[S_3]=\mathbb{R}\cdot(1)+\mathbb{R}\cdot(12)+\mathbb{R}\cdot(13)+\mathbb{R}\cdot(23)+\mathbb{R}\cdot(123)+\mathbb{R}\cdot(132)$$
a.) Find the center ##Z(A)=\{\,z \in A\,|\,zv=vz\text{ for all }v\in A\,\}## of ##A##, and
b.) determine the structure of ##A##, i.e. its decomposition into direct factors and the corresponding isomorphisms.
9.) Let ##B\subseteq \mathbb{R}^n## be measurable and ##P=(a_1,\ldots,a_n,b)\in \mathbb{R}^{n+1}## a point with ##b>0## and ##C_B=\{\,P+t(Q-P)\,|\,Q\in B\times \{0\}_{n+1}\, , \,t\in [0,1]\,\}## the cone above the basis ##B## with the peak ##P\,.##
Prove the measure formula
$$
\lambda^{n+1}(C_B)=\dfrac{b}{n+1}\cdot \lambda^n(B)
$$
10.) Show that $$
x \cdot y = \frac{2xy-x-y}{xy-1}$$
defines a one dimensional, real, local Lie group ##G## around ##0 \in \mathbb{R}## and compute the vector field of left multiplication by an element ##g \in \mathbb{R}##.
 1.) (solved by @fbs7 ) Find the limit of the sequence ##a_n = 2\cdot \sqrt[3]{4}\cdot \sqrt[9]{16}\cdot \sqrt[27]{256} \,\cdots \, \sqrt[3^{n-1}]{2^{2^{n-1}}}##.
1.) (solved by @fbs7 ) Find the limit of the sequence ##a_n = 2\cdot \sqrt[3]{4}\cdot \sqrt[9]{16}\cdot \sqrt[27]{256} \,\cdots \, \sqrt[3^{n-1}]{2^{2^{n-1}}}##.
2.) Let ##(b_n)## be a sequence with ##b_n = \dfrac{nn^n}{(n!)^2}##.
a.) Show that ##(b_n)## converges and find its limit.
b.) Using the above find the limit of the sequence ##(a_n)## with ##a_n = \dfrac{1^n + 2^n + 3^n + \dots + n^n}{(n!)^2}##.
3.) (solved by @fbs7 ) Two numbers ##a,b## are called amicable, if the sum of all proper divisors of one is the other number (##1## is included). The smallest example is
$$
(a,b) = (220,284)=(1+2+4+71+142,1+2+4+5+10+11+20+22+44+55+110)
$$
Let ##n\in \mathbb{N}## and ##(x,y,z)=\left(3\cdot 2^n-1\, , \,3\cdot 2^{n-1}-1\, , \,9\cdot 2^{2n-1}-1\right)\,.##
Prove that if ##x,y,z## are all odd primes, then ##(a,b)=\left( 2^n\cdot x\cdot y\,,\, 2^n\cdot z \right)## are amicable numbers.
Hint: First find a formula for the sum of all divisors ##\sigma(n)## given the prime decomposition of ##n##.
4.) (solved by @fbs7 ) A number is called perfect, if it equals the number of all its divisors except itself, e.g. ##6=1+2+3## and ##28=1+2+4+7+14## are perfect.
Prove: If ##2^k-1## is a prime number, then ##2^{k-1}(2^k-1)## is a perfect number and every even perfect number has this form.
5.) a.) (solved by @fbs7 ) What is the smallest five-digit number ##n## such that ##n## and ##2n## together contain all ##10## digits from ##0## to ##9##?
b.) (solved by @fbs7 ) On how many zeros does the number ##1000\,!## end?
c.) (solved by @fbs7 ) For which six-digit number ##ABCDEF## do we have:
##ABCDEF \cdot 1 = ABCDEF##
##ABCDEF \cdot 3 = BCDEFA##
##ABCDEF \cdot 2 = CDEFAB##
##ABCDEF \cdot 6 = DEFABC##
##ABCDEF \cdot 4 = EFABCD##
##ABCDEF \cdot 5 = FABCDE##
1.) (disclosed by @Demystifier ) Using the notion of double integrals prove that $$B(m,n) = \frac{\Gamma (m) \Gamma (n)}{\Gamma (m + n)}\; \;(m \gt 0\,,\, n\gt 0)$$ where ##B## and ##\Gamma## are the Beta and Gamma functions respectively.
2.) (solved by @Math_QED ) Show that the Fourier series of an even function cannot contain sine.
3.) (solved by @Bosko ) Show that $$\int_{0}^{1} dx \int_{x}^{\sqrt{x}} f(x,y)\,dy = \int_{0}^{1} dy \int_{y^2}^{y} f(x,y)\,dx\,.$$
4.) The graphic of eye colors shows us the probability of baby's eye color in dependency of the parents'. This yields the following multiplication table:
\begin{align*}
x \cdot x &= (3/4) x + (3/16) y + (1/16) z\\
x \cdot y &=(1/2) x+(3/8) y+(1/8) z\\
x \cdot z &=(1/2) x+(1/2) z\\
y \cdot y &=(3/4) y+(1/4) z\\
y \cdot z &=(1/2) y+(1/2) z\\
z \cdot z &= z
\end{align*}
which we extend to a real, commutative, distributive, three dimensional algebra ##A##.
a) (solved by @fbs7 ) Is ##A## an associative algebra?
still open:
b) Prove, that ##A## is a baric algebra, i.e. show that there is a non trivial algebra homomorphismus ##\omega\, : \,A\longrightarrow \mathbb{R}##, the weight function.
c) Determine a basis for ##\operatorname{ker}\omega## and rewrite the multiplication table according to this new basis.
d) Prove that there is an ideal ##N## of codimension one in ##A##, such that ##A^2 \nsubseteq N##.
e) A algebra is called genetic, if there is a basis ##\{\,u_i\,\}## such that the structure constants ##\lambda_{ijk}## defined by
$$
u_i \cdot u_j = \sum_{k=1}^n \lambda_{ijk}u_k
$$
fulfill the following conditions:
- ##\lambda_{111}=1##
- ##\lambda_{1jk}=0## for all ##j>k##
- ##\lambda_{ijk}=0## for all ##i,j > 1## and ##k \leq \operatorname{max}\{i,j\}##
f) Show that ##A## is not a genetic algebra.
g) Determine all idempotent elements of ##A##. Is there a basis of ##A## with idempotent elements?
5.) (solved by @Bosko ) Prove that starting with ##\frac{1}{1}## the following binary tree
$$
\begin{array}{ccccc}
&&\frac{a}{b}&&\\
&\swarrow &&\searrow \\
\frac{a}{a+b}&&&&\frac{a+b}{b}
\end{array}
$$
defines a counting of all positive rational numbers without repetition and all quotients canceled out.
6.) (solved by @Cthugha ) Who said what here? (What is the task, who a bonus.)
7.) (solved by @lpetrich ) Calculate ##I:=\int_0^\infty \dfrac{\sqrt{x^{e-2}}}{x^e+1}\,dx##
8.) An algebra ##A## is a vector space with a binary distributive multiplication. An example are group algebras, i.e. the distributive extension of the formal basis vectors ##g\in G## such as $$A :=\mathbb{R}[S_3]=\mathbb{R}\cdot(1)+\mathbb{R}\cdot(12)+\mathbb{R}\cdot(13)+\mathbb{R}\cdot(23)+\mathbb{R}\cdot(123)+\mathbb{R}\cdot(132)$$
a.) Find the center ##Z(A)=\{\,z \in A\,|\,zv=vz\text{ for all }v\in A\,\}## of ##A##, and
b.) determine the structure of ##A##, i.e. its decomposition into direct factors and the corresponding isomorphisms.
9.) Let ##B\subseteq \mathbb{R}^n## be measurable and ##P=(a_1,\ldots,a_n,b)\in \mathbb{R}^{n+1}## a point with ##b>0## and ##C_B=\{\,P+t(Q-P)\,|\,Q\in B\times \{0\}_{n+1}\, , \,t\in [0,1]\,\}## the cone above the basis ##B## with the peak ##P\,.##
Prove the measure formula
$$
\lambda^{n+1}(C_B)=\dfrac{b}{n+1}\cdot \lambda^n(B)
$$
10.) Show that $$
x \cdot y = \frac{2xy-x-y}{xy-1}$$
defines a one dimensional, real, local Lie group ##G## around ##0 \in \mathbb{R}## and compute the vector field of left multiplication by an element ##g \in \mathbb{R}##.
2.) Let ##(b_n)## be a sequence with ##b_n = \dfrac{nn^n}{(n!)^2}##.
a.) Show that ##(b_n)## converges and find its limit.
b.) Using the above find the limit of the sequence ##(a_n)## with ##a_n = \dfrac{1^n + 2^n + 3^n + \dots + n^n}{(n!)^2}##.
3.) (solved by @fbs7 ) Two numbers ##a,b## are called amicable, if the sum of all proper divisors of one is the other number (##1## is included). The smallest example is
$$
(a,b) = (220,284)=(1+2+4+71+142,1+2+4+5+10+11+20+22+44+55+110)
$$
Let ##n\in \mathbb{N}## and ##(x,y,z)=\left(3\cdot 2^n-1\, , \,3\cdot 2^{n-1}-1\, , \,9\cdot 2^{2n-1}-1\right)\,.##
Prove that if ##x,y,z## are all odd primes, then ##(a,b)=\left( 2^n\cdot x\cdot y\,,\, 2^n\cdot z \right)## are amicable numbers.
Hint: First find a formula for the sum of all divisors ##\sigma(n)## given the prime decomposition of ##n##.
4.) (solved by @fbs7 ) A number is called perfect, if it equals the number of all its divisors except itself, e.g. ##6=1+2+3## and ##28=1+2+4+7+14## are perfect.
Prove: If ##2^k-1## is a prime number, then ##2^{k-1}(2^k-1)## is a perfect number and every even perfect number has this form.
5.) a.) (solved by @fbs7 ) What is the smallest five-digit number ##n## such that ##n## and ##2n## together contain all ##10## digits from ##0## to ##9##?
b.) (solved by @fbs7 ) On how many zeros does the number ##1000\,!## end?
c.) (solved by @fbs7 ) For which six-digit number ##ABCDEF## do we have:
##ABCDEF \cdot 1 = ABCDEF##
##ABCDEF \cdot 3 = BCDEFA##
##ABCDEF \cdot 2 = CDEFAB##
##ABCDEF \cdot 6 = DEFABC##
##ABCDEF \cdot 4 = EFABCD##
##ABCDEF \cdot 5 = FABCDE##
Last edited:
