Transactions & schedules - Dependency relations

[mathmari]

Hey! :giggle:

The below transactions are given :

and the below schedules :

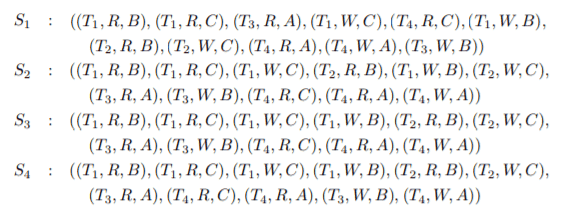
Give the respective dependency relations as well as the precedence graphs. Which schedules are conflict serializable? Which schedules are equivalent?



I reread some notes and looked also for some examples in Google and now I have done the following :

Are the below dependent in $S_1$ ?
$(T_1, R, B) \to (T_3, W,B)$
$(T_1, R, C) \to (T_2, W, C)$
$(T_3, R, A) \to (T_4, W, A)$
$(T_1, W, C) \to (T_4, R, C)$
$(T_4, R, C) \to (T_2, W, C)$
$(T_1, W, B) \to (T_3, W, B)$
$(T_2, R, B) \to (T_3, W, B)$

Then we would get \begin{align*}\text{DEP}(S_1)&=\{(T_1,B,T_3), (T_1, C, T_2), (T_3, A, T_4), (T_1, C, T_4), (T_4, C, T_2), (T_1, B, T_3), (T_2, B, T_3)\}\\ & =\{(T_1,B,T_3), (T_1, C, T_2), (T_3, A, T_4), (T_1, C, T_4), (T_4, C, T_2), (T_2, B, T_3)\}\end{align*}

Is that correct? :unsure:


If that is correct then for the other schedules we have :

The dependent ones in $S_2$ are :
$(T_1, R, B) \to (T_3, W,B)$
$(T_1, R, C) \to (T_2, W, C)$
$(T_1, W, C) \to (T_2, W, C)$
$(T_2, R, B) \to (T_1, W, B)$
$(T_1, W, B) \to (T_3, W, B)$
$(T_2, W, C) \to (T_4, R, C)$
$(T_3, R, A) \to (T_4, W, A)$

Then we would get \begin{align*}\text{DEP}(S_2)&=\{(T_1,B,T_3), (T_1, C, T_2), (T_1, C, T_2), (T_2, B, T_1), (T_1, B, T_3), (T_2, C, T_4), (T_3, A, T_4)\}\\ &=\{(T_1,B,T_3), (T_1, C, T_2), (T_2, B, T_1), (T_2, C, T_4), (T_3, A, T_4)\}\end{align*}



The dependent ones in $S_3$ are :
$(T_1, R, B) \to (T_3, W,B)$
$(T_1, R, C) \to (T_2, W, C)$
$(T_1, W, C) \to (T_2, W, C)$
$(T_1, W, B) \to (T_2, R, B)$
$(T_2, R, B) \to (T_3, W, B)$
$(T_2, W, C) \to (T_4, R, C)$
$(T_3, R, A) \to (T_4, W, A)$

Then we would get \begin{align*}\text{DEP}(S_3)&=\{(T_1,B,T_3), (T_1, C, T_2), (T_1, C, T_2), (T_1, B, T_2), (T_2, B, T_3), (T_2, C, T_4), (T_3, A, T_4)\}\\ & =\{(T_1,B,T_3), (T_1, C, T_2), (T_1, B, T_2), (T_2, B, T_3), (T_2, C, T_4), (T_3, A, T_4)\}\end{align*}



The dependent ones in $S_4$ are :
$(T_1, R, B) \to (T_3, W,B)$
$(T_1, R, C) \to (T_2, W, C)$
$(T_1, W, C) \to (T_2, W, C)$
$(T_1, W, B) \to (T_2, R, B)$
$(T_2, R, B) \to (T_3, W, B)$
$(T_2, W, C) \to (T_4, R, C)$
$(T_3, R, A) \to (T_4, W, A)$

Then we would get \begin{align*}\text{DEP}(S_4)&=\{(T_1,B,T_3), (T_1, C, T_2), (T_1, C, T_2), (T_1, B, T_2), (T_2, B, T_3), (T_2, C, T_4), (T_3, A, T_4)\}\\ & =\{(T_1,B,T_3), (T_1, C, T_2), (T_1, B, T_2), (T_2, B, T_3), (T_2, C, T_4), (T_3, A, T_4)\}\end{align*}


Is everything correct so far? :unsure:


From the precedence graphs we check which are acyclic and these ones are conflict serializable, right?
So $S_3$ and $S_4$ are conflict serializable, right? :unsure:


We have that $\text{DEP}(S_3)=\text{DEP}(S_4)$. We have to check if $S_3$and $S_4$ have the same transactions so that we can say that these two schedules are equivalent, right? But exactly does it mean that they have the same transactions? Is it maybe that the schedules $S_3$ and $S_4$ are the same if we reorder some elements? Is that the desired condition that we need? :unsure:

 

[mathmari]

The notes that I am looking at are these ones from the end of the pdf-page 87.