Optimization with Lagrangian Multipliers

[Leo Liu]

Homework Statement

.

Relevant Equations

$\nabla f=\lambda\nabla g$

Problem:

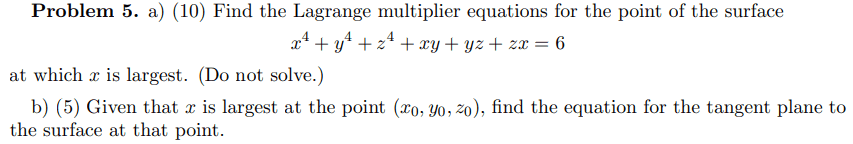
Solution:

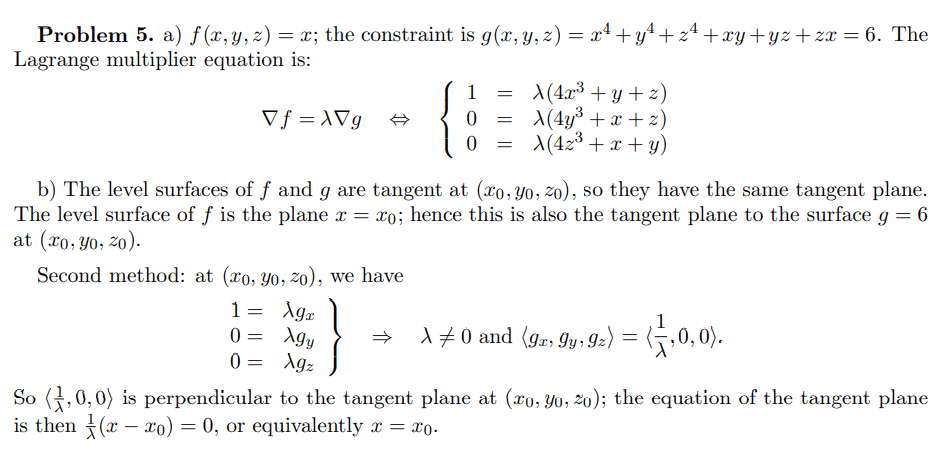
My question:
My reasoning was that if x is max at the point then the gradient vector of g at the point has only x component; that is $g_y=0,\, g_z=0$. This way I got:
$$\begin{cases}
4y^3+x+z=0\\
\\
4z^3+x+y=0\\
\\
\underbrace{x^4+y^4+z^4+xy+yz+zx=6}_\text{constraint equation}
\end{cases}$$
which produces the same solutions as the list of equations in the official answer does.

What puzzles me is why the answer defines that $f(x,y,z)=x$. I understand the gradient vector should be parallel to the vector $<1,0,0>$, and therefore the equation f is x. But this step is reverse engineered. Can someone please explain where $f(x,y,z)=x$ comes from?

Many thanks.

 

[etotheipi]

Can someone please explain where $f(x,y,z)=x$ comes from?

That's just the function you're extremising, $f(\boldsymbol{x}) = x$ (i.e. the function taking a point $\in \mathbb{R}^3$ to its $x$ co-ordinate, which is what you're trying to maximise) subject to the constraint $g(\boldsymbol{x}) = 6$. It's essentially by construction.

To give some more context, the constraint defines a 2-dimensional surface with normal vector $\nabla g(\boldsymbol{x})$; displacements $\mathrm{d}\boldsymbol{x}$ within this surface must satisfy $\mathrm{d}\boldsymbol{x} \cdot \nabla g (\boldsymbol{x} )= 0$, i.e. they must be parallel to the surface. Furthermore, if $\boldsymbol{x}_0$ is the point corresponding to the extremum of $f(\boldsymbol{x})$ under the given constraint, you must have $\mathrm{d}\boldsymbol{x} \cdot \nabla f (\boldsymbol{x}_0) = 0$, since the change in the value of the function will be zero to first order under a displacement $\mathrm{d}\boldsymbol{x}$. The only way these two things are possible is if $$\nabla f(\boldsymbol{x}_0) = \lambda \nabla g(\boldsymbol{x}_0)$$It's because if they were not parallel, you would have$$\nabla f(\boldsymbol{x}_0) = \lambda \nabla g(\boldsymbol{x}_0) + \mathbf{a}(\boldsymbol{x}_0) \implies \mathrm{d}\boldsymbol{x} \cdot \nabla f(\boldsymbol{x}_0) = \mathrm{d}\boldsymbol{x} \cdot \mathbf{a}(\boldsymbol{x}_0)$$for some $\mathbf{a}(\boldsymbol{x}_0)$ which is perpendicular to $\nabla g(\boldsymbol{x}_0)$. But since $\mathrm{d}\boldsymbol{x}$ can be a displacement of any direction in the constraint surface, we can consider letting $\mathrm{d}\boldsymbol{x} = \mathbf{a}(\boldsymbol{x}_0) \mathrm{d}s$, in which case $\mathrm{d}\boldsymbol{x} \cdot \mathbf{a}(\boldsymbol{x}_0) = |\mathbf{a}(\boldsymbol{x}_0)|^2 \mathrm{d}s > 0$, which means that $\mathrm{d}\boldsymbol{x} \cdot \nabla f(\boldsymbol{x}_0)$ would no longer be zero.