Vibhor
- 971
- 40
I am facing difficulty in understanding a key point . Hence I am putting it here instead of Introductory Physics section .
Here is a part of the solution provided by the teacher ,but it doesn't look convincing to me.
Similar solution is provided here http://www.phy.duke.edu/~dtl/136126/36h2_sho.html
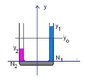
Line marked in red is what I don't understand . I feel that the restoring force acts only on the fluid of length l-2y ,whereas the solution says that the restoring force acts on the entire liquid .
Could somebody please explain this to me ?
Many thanks
Here is a part of the solution provided by the teacher ,but it doesn't look convincing to me.
Similar solution is provided here http://www.phy.duke.edu/~dtl/136126/36h2_sho.html
Solution - The liquid of length l is in the U-tube .If a compressive force is applied in one arm and it displace water by depth y in the same arm.
In the result difference in the liquid level in the tube = 2y.
The weight of the liquid present in this level 2y provides the necessary restoring force. So when the compressing force is removed the liquid tries to come back to its equilibrium position but due to inertia overshoots this position and thus starts oscillating.
Restoring force = - (2yAρ)g
It tries to bring the liquid back to its equilibrium position and thus acts on the whole of liquid present in the U-tube. Thus restoring acceleration is given by
If a compressive force is applied in one arm and it displace water by depth y in the same arm.
In the result difference in the liquid level in the tube = 2y.
The weight of the liquid present in this level 2y provides the necessary restoring force. So when the compressing force is removed the liquid tries to come back to its equilibrium position but due to inertia overshoots this position and thus starts oscillating.
Restoring force = - (2yAρ)g
It tries to bring the liquid back to its equilibrium position and thus acts on the whole of liquid present in the U-tube.
Line marked in red is what I don't understand . I feel that the restoring force acts only on the fluid of length l-2y ,whereas the solution says that the restoring force acts on the entire liquid .
Could somebody please explain this to me ?
Many thanks