Oscillation with 2 springs attached to a mass

[link223]

Homework Statement

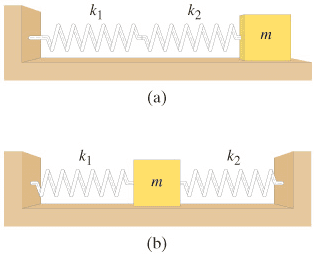
A mass m is connected to two springs, with spring constants k1 and k2 , in two different ways as shown in the figure.
Find the period for the configuration shown in the figure (a). Ignore friction.
Find the period for the configuration shown in the figure (b).
Express your answer in terms of the variables m, k1 , k2 and appropriate constants.

Relevant Equations

I don't know

How in the world I am supposed to start with this problem?
No clue, so can't provide HW solution by any means.
regards.

 

[erobz]

I'd start with free body diagrams, and a coordinate system.

 

[Doc Al]

How in the world I am supposed to start with this problem?

Can you solve the simpler problem of a mass attached to a single spring?

(You really need to show something of your thinking here, so we have a clue where you are getting stuck.)

 

[Delta2]

The general idea is to replace the two springs with one spring of constant $k=f(k_1,k_2)$ where f is a proper function different in each of the cases (a), (b).
Lets start to do this with case (b) which I consider simpler. Suppose mass m travels $x$ distance to the right. What is the total force on mass m at that point?

 

[erobz]

I don't know if there is a better way, but I put my coordinate system $x = 0$ at the leading edge of the block in scenario $a$ where it attaches to spring $2$. Then I'd see if you can relate the displacement $x$ to the individual lengths of the springs $x_1$ and $x_2$. That should get you started on $a$.

 

[haruspex]

The question ought to state that in b) both springs are relaxed at the equilibrium position. Otherwise it cannot be solved.

 

[Steve4Physics]

The question ought to state that in b) both springs are relaxed at the equilibrium position. Otherwise it cannot be solved.

For part b), I don’t think there is a requirement for the springs to be relaxed at the equilibrium position.

Suppose the mass is in equilibrium when the springs are both in (say) tension, with extensions $e₁$ and $e₂$.
$-k₁e₁ + k₂e₂= 0$

If the mass is displaced by $\Delta x$, the resultant (restoring) force, $F$, on the mass is:
$\begin{align*} F &= -k₁(e₁ + \Delta x) + k₂(e₂ - \Delta x) \\ &= -k₁e₁ +k₂e₂ – k₁\Delta x - k₂\Delta x\\ &= 0 - (k₁+k₂)\Delta x \end{align*}$

So the restoring force (and hence the period of oscillation) is independent of $e₁$ and $e₂$.

 

[kuruman]

For part b), I don’t think there is a requirement for the springs to be relaxed at the equilibrium position.

Suppose the mass is in equilibrium when the springs are both in (say) tension, with extensions $e₁$ and $e₂$.
$-k₁e₁ + k₂e₂= 0$

If the mass is displaced by $\Delta x$, the resultant (restoring) force, $F$, on the mass is:
$\begin{align*} F &= -k₁(e₁ + \Delta x) + k₂(e₂ - \Delta x) \\ &= -k₁e₁ +k₂e₂ – k₁\Delta x - k₂\Delta x\\ &= 0 - (k₁+k₂)\Delta x \end{align*}$

So the restoring force (and hence the period of oscillation) is independent of $e₁$ and $e₂$.

I was going to post the same objection, but you preempted me. Based on past experience, I believe that @haruspex has cultivated the ability to see what's in others' blind spots. So let's wait for his response.

 

[erobz]

I hope the OP makes an effort here, I look forward to maybe seeing a few ways to approach this, and maybe clear up some concerns I myself am having in solving part a.

 

[haruspex]

For part b), I don’t think there is a requirement for the springs to be relaxed at the equilibrium position.

Suppose the mass is in equilibrium when the springs are both in (say) tension, with extensions $e₁$ and $e₂$.
$-k₁e₁ + k₂e₂= 0$

If the mass is displaced by $\Delta x$, the resultant (restoring) force, $F$, on the mass is:
$\begin{align*} F &= -k₁(e₁ + \Delta x) + k₂(e₂ - \Delta x) \\ &= -k₁e₁ +k₂e₂ – k₁\Delta x - k₂\Delta x\\ &= 0 - (k₁+k₂)\Delta x \end{align*}$

So the restoring force (and hence the period of oscillation) is independent of $e₁$ and $e₂$.

Next time I'll have my coffee first.

 

[Delta2]

I think @Steve4Physics has a little mistake, the total force is $$F=-k_1(e_1+\Delta x)-k_2(e_2-\Delta x)$$ which will result in $$F=-(k_1-k_2)\Delta x$$.

 

[haruspex]

I think @Steve4Physics has a little mistake, the total force is $$F=-k_1(e_1+\Delta x)-k_2(e_2-\Delta x)$$ which will result in $$F=-(k_1-k_2)\Delta x$$.

No, it is +k₂, as Steve wrote.

 

[Delta2]

No, it is +k₂, as Steve wrote.

isn't the force from each spring $-k_ix_i$ $i=1,2$. Why do we take the force from 2nd spring as $k_2x_2$ without the minus sign?

 

[haruspex]

isn't the force from each spring $-k_ix_i$ $i=1,2$. Why do we take the force from 2nd spring as $k_2x_2$ without the minus sign?

Because it acts in the opposite direction. If the body moves right the left spring increases in length, adding force to the left, while the other spring reduces in length, also adding force to the left.

 

[Steve4Physics]

I think @Steve4Physics has a little mistake, the total force is $$F=-k_1(e_1+\Delta x)-k_2(e_2-\Delta x)$$ which will result in $$F=-(k_1-k_2)\Delta x$$.

Hi @Delta. In case of any remaining doubt...

Consinder the case where both springs are in tension:
Spring-1 pulls the mass to the left, so this force is negative.
Spring 2-pulls the mass to the right, so this force is positive.

Also, ‘$F=-(k_1-k_2)\Delta x$’ would mean that if we used equal stiffness springs ($k_1=k_2$) the net force would be zero, so no oscillations would be possible.

 

[Delta2]

Consinder the case where both springs are in tension:
Spring-1 pulls the mass to the left, so this force is negative.
Spring 2-pulls the mass to the right, so this force is positive.

actually if spring 1 pulls the mass to the left, then spring 2 pushes the mass to the left, so both forces are positive.

 

[Steve4Physics]

actually if spring 1 pulls the mass to the left, then spring 2 pushes the mass to the left, so both forces are positive.

Spring 2 can only push the mass to the left when the spring is in a state of compression.

That’s why I said “Consider the case where both springs are in tension”.

Of course, if $|\Delta x|$ is large enough, then during the motion each of the springs could become temporarily compressed. But that doesn’t affect the construction of the equation:
$F=-k_1(e_1+\Delta x)+k_2(e_2-\Delta x)$

For example, if $\Delta x$ is large enough, then spring -2 could become compressed and the expression $(e_2-\Delta x)$ automatically becomes negative to take this into account.

 

[Delta2]

Spring 2 can only push the mass to the left when the spring is in a state of compression.

That’s why I said “Consider the case where both springs are in tension”.

Of course, if $|\Delta x|$ is large enough, then during the motion each of the springs could become temporarily compressed. But that doesn’t affect the construction of the equation:
$F=-k_1(e_1+\Delta x)+k_2(e_2-\Delta x)$

For example, if $\Delta x$ is large enough, then spring -2 could become compressed and the expression $(e_2-\Delta x)$ automatically becomes negative to take this into account.

Yes ok thanks, I see what you mean now, in my mind I had for granted that both springs start at their natural length so if spring 1 is elongated, then spring 2 is compressed and vice versa.

 

[bob012345]

The net force for small displacements is the same for all three possible cases of both springs equilibrium starting conditions of natural length, tension or compression.

 

[Steve4Physics]

The net force for small displacements is the same for all three possible cases of both springs equilibrium starting conditions of natural length, tension or compression.

Yes. The displacements don't even have to be small - providing both springs obey Hooke's law.

 

[Doc Al]

Gang: You guys are killing me. Please realize that this is the HW forum and the OP hasn't posted anything since the problem statement.