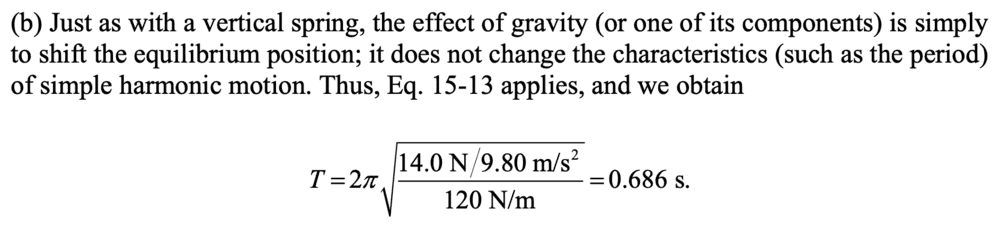SUMMARY
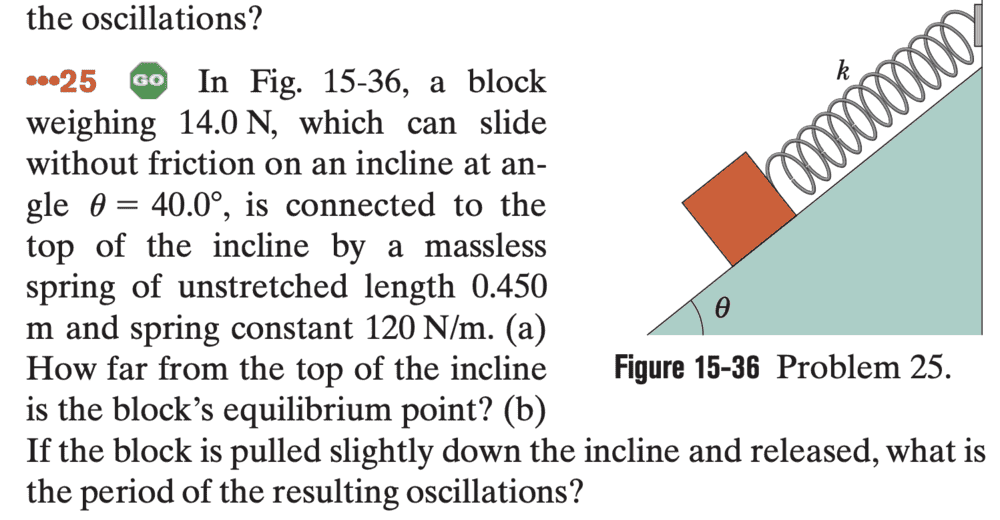
The discussion centers on the oscillation of a block mass attached to a spring on an incline, specifically addressing why the incline angle does not affect the mass component in the oscillation period equation, ##T = 2π\sqrt{\frac{m}{k}}##. It concludes that both the mass and the spring experience the same gravitational force, leading to identical equations of motion regardless of the incline angle. The analysis demonstrates that the only effect of weight is to alter the equilibrium position, not the oscillation characteristics, confirming that oscillation periods remain consistent across different angles.
PREREQUISITES
- Understanding of harmonic motion and oscillation principles
- Familiarity with Hooke's Law and spring constants (k)
- Basic knowledge of differential equations in physics
- Concept of equilibrium positions in mechanical systems
NEXT STEPS
- Study the derivation of the oscillation period for different spring configurations
- Explore the effects of varying mass on oscillation frequency in spring systems
- Learn about the dynamics of oscillations on inclined planes
- Investigate the role of damping in oscillatory motion of springs
USEFUL FOR
Students and educators in physics, mechanical engineers, and anyone interested in the dynamics of oscillatory systems and spring mechanics.