Oscillator circuit. completely lost.

[raindrops]

Homework Statement

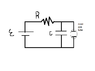
An oscillator circuit is important to many applications. A simple oscillator circuit can be built by adding a neon gas tube to an RC circuit, as shown in the figure below. Gas is normally a good insulator, and the resistance of the gas tube is essentially infinite when the light is off. This allows the capacitor to charge. When the capacitor voltage reaches a value Von, the electric field inside the tube becomes strong enough to ionize the neon gas. Visually, the tube lights with an orange glow. Electrically, the ionization of the gas provides a very-low-resistance path through the tube. The capacitor very rapidly (we can think of it as instantaneously) discharge through the tube and the capacitor voltage drops. When the capacitor voltage has dropped to a value of Voff, the electric field inside the tube becomes too weak to sustain the ionization and the neon light turns off. The capacitor then starts to charge again. The capacitor voltage oscillates between Voff, when it starts chargin, and Von, when the light comes on to discharge it.

a) Make a graph of the Vc (voltage across the capacitor) vs. time, with the capacitor initially having no charge.
b) Show that the oscillation period is T=RC ln($$E$$-Voff)/($$E$$-Von)
c) A neon gass tube has Von= 80V and Voff = 20V. What resistor value should you choose to go with a 10$$\mu$$F capacitor and a 90V battery to make a 10Hz oscillator?


(** attachment has pic)



I really would just like some help getting this started. I'm completely lost as to where to go or what equations to use. Any insight and direction would be great. Thanks.

 

[cnh1995]

a) Make a graph of the Vc (voltage across the capacitor) vs. time, with the capacitor initially having no charge.

Capacitor will be charged to V_on exponentially and will be suddenly discharged( instantaneously) to V_off, and this cycle will go on. In the very beginning, since the charge on the capacitor is 0, charging voltage waveform will be 0 to V_on but for the rest of the time, it will be from V_off to V_on and straight back to V_off. I am sorry I can't draw and upload the waveform now but this is what the nature of the waveform will be..

b) Show that the oscillation period is T=RC ln(E-Voff)/(E-Von)

Time period of the wave will be only the charging time of the capacitor (since it discharges instantaneously).In the steady state, the capacitor will be charged to V_on from initial voltage V_off. So, voltage across the capacitor during charging can be written as,
V_c=V_off +(E-V_off)*(1-e^-t/RC).
At t=T, Vc=V_on
∴(Von-Voff)/(E-Voff)=1-e^-T/RC
∴e^-T/RC=1-[(Von-Voff)/(E-Voff)]
=(E-Von)/(E-Voff)
Taking natural log on both sides,
-T/RC=ln[(E-Von)/(E-Voff)]
T=RCln[(E-Voff)/(E-Von)]

c) A neon gass tube has Von= 80V and Voff = 20V. What resistor value should you choose to go with a 10

μμ​

\muF capacitor and a 90V battery to make a 10Hz oscillator?

Plug these values in the above equation and solve for R.