Partial capacitances of a system of conductors

[Granger]

Homework Statement

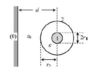
I have a small question about the following problem. The figure represents the cross-section of a three-conductor system comprising a communications coaxial cable of length l running parallel to a conducting wall (reference conductor). Determine the partial capacitance scheme of the conductor system.

[![enter image description here][1]][1] [1]: https://i.stack.imgur.com/G0l6u.png

Homework Equations

3. The Attempt at a Solution [/B]

So, I had zero troubles finding out the capacitance between conductor 2 and zero and between conductor 1 and 2.

$$ C_{20} = \frac{2 \pi \epsilon_0 l}{\ln (\frac{d}{r_2} + \sqrt{(\frac{d}{r_2})^2 -1})}$$

$$ C_{12} = \frac{2 \pi \epsilon l}{\ln (\frac{r_2}{r_1})}$$

However I'm having trouble understanding why $$ C_{10} = 0 $$. My guess is that somehow conductor 2 acts as an electric shield between conductor 1 and conductor zero, so that the electric field due to conductor 1 is not "felt" by conductor zero. However I'm not sure if this is correct and would like some more insight about this. Can someone help me?

 

[berkeman]

Hmm, that doesn't look right to me either. From an EE perspective, C12 and C20 are in series to form C10... I'm not familiar with the term "partial capacitance" though -- maybe it has some other meaning?

 

[Granger]

Hmm, that doesn't look right to me either. From an EE perspective, C12 and C20 are in series to form C10... I'm not familiar with the term "partial capacitance" though -- maybe it has some other meaning?

Hey berkeman! Thank you for trying to help.
Yes partial capacitances are a little bit different than "regular capacitances" (i.e. the capacitances that figure out on a capacitance matrix). What my book says is

" An alternative method – the so-called partial capacitance scheme – consists of modeling theelectric interactions among conductors through a network of n(n+1)/2 fictitious capacitors. Physically speaking, each capacitor connecting any two conductors is intended somehow to represent the electric field lines existing between those conductors. The electric energy stored in the multiple conductor system is the sum of the electric energies pertaining to the capacitors of the scheme."

I'll provide an example if you need one.
That's why I think they're right when they say the partial capacitance C10 is zero because there are no field lines that go from conductor 1 through conductor 0 (only between conductors 1 and 2 and conductors 2 and zero) because the conducting shell acts as a shield. What do you think?

EDIT: Because in the next question we are supposed to relate the partial capacitances to the actual capacitances and C10 is indeed different than zero

 

[berkeman]

That's why I think they're right when they say the partial capacitance C10 is zero because there are no field lines that go from conductor 1 through conductor 0 (only between conductors 1 and 2 and conductors 2 and zero) because the conducting shell acts as a shield. What do you think?

Yes, okay, that all makes sense now. You are correct that there are no field lines starting on 1 and ending on 0.