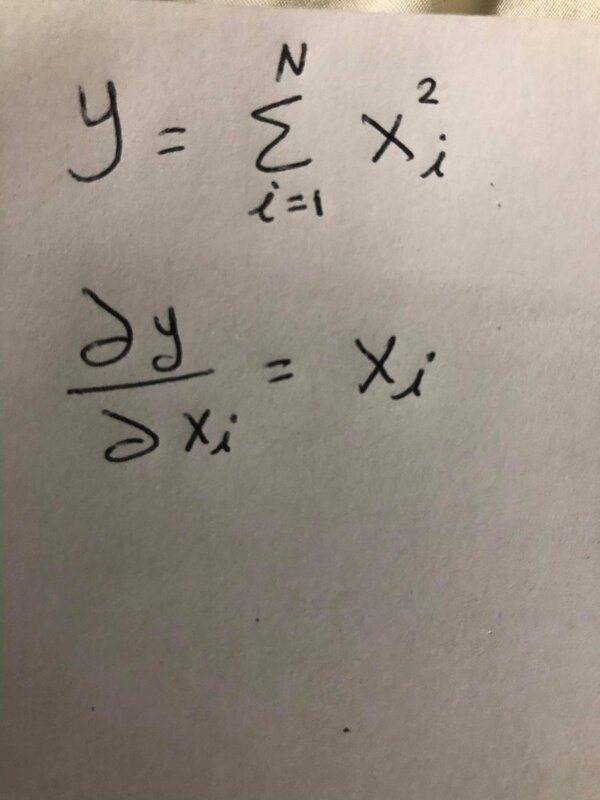SUMMARY
The discussion centers on the cancellation of terms in the summation when taking the partial derivative with respect to a specific variable, denoted as x_i. Participants clarify that when differentiating the sum of squares, only the term corresponding to x_i contributes to the derivative, resulting in the expression 2x_i. The key takeaway is that all other terms yield zero due to the independence of the variables, confirming that the summation simplifies effectively during differentiation.
PREREQUISITES
- Understanding of partial derivatives in calculus
- Familiarity with summation notation and its properties
- Knowledge of independent variables in mathematical functions
- Basic proficiency in algebraic manipulation
NEXT STEPS
- Study the properties of partial derivatives in multivariable calculus
- Learn about the chain rule and its application in differentiation
- Explore the concept of linearity in differentiation
- Investigate the implications of variable independence in calculus
USEFUL FOR
Students of mathematics, educators teaching calculus, and professionals in fields requiring advanced mathematical analysis will benefit from this discussion.