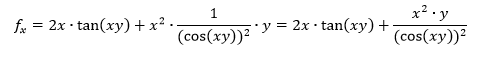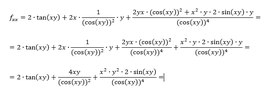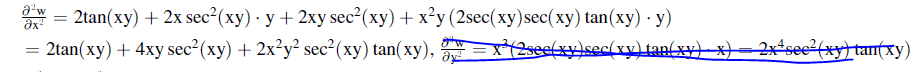Partial Derivative of f(x,y): Solving with Maple & Book

[Yankel]

Hello all,

I am trying to calculate the second order of the partial derivative by x of the function:

f(x,y)=(x^2)*tan(xy)

In the attach images you can see my work.

Both the answer in the book where it came from and maple say that the answer is almost correct, but not entirely. In the last fracture in the answer, they say it should be cos(xy)^2, while in my answer is seems to be cos(xy)^3.

I can't figure out what I am doing wrong...

I am attaching also the answer from the book.

Thank you !

 

[MarkFL]

We are given:

$$f(x,y)=x^2\tan(xy)$$

Hence:

$$f_{x}(x,y)=x^2\left(\sec^2(xy)(y) \right)+2x\tan(xy)=x^2y\sec^2(xy)+2x\tan(xy)$$

and so:

$$f_{xx}(x,y)=\left(x^2y \right)\left(2\sec(xy)\left(\sec(xy)\tan(xy) \right)(y) \right)+(2xy)\sec^2(xy)+(2x)\left(\sec^2(xy)(y) \right)+2\tan(xy)=$$

$$2x^2y^2\sec^2(xy)\tan(xy)+4xy\sec^2(xy)+2\tan(xy)$$

 

[Yankel]

thank you, can you please show me where was the mistake in my solution ?

because I just did it again for the second order derivative by y...I always get 3rd power when it's 2nd, I can't find out what I am doing wrong

 

[Fantini]

I am a bit confused by the images. I have the feeling the ones with $f_x$ and $f_{xx}$ are your work, whereas the one with $\partial^2 w / \partial x^2$ is from the book. I'm having a hard time figuring out then where you could have gone wrong, so I'll spell out the passages and we can work together to find out where you went astray. :)

For the first partial derivative we have

$$
\begin{align}
f_x & = \frac{\partial}{\partial x} x^2 \tan (xy) \\
& = 2x \tan (xy) + x^2 \sec^2 (xy) \cdot y.
\end{align}
$$

For the second partial derivative we have

$$
\begin{align}
f_{xx} & = 2 \tan (xy) + 2x \sec^2 (xy) \cdot y + 2xy \sec^2 (xy) + x^2 y \cdot (2 \sec (xy)) \cdot \tan (xy) \cdot \sec (xy) \cdot y \\
& = 2 \tan (xy) + 4xy \sec^2 (xy) + 2 (xy)^2 \sec^2 (xy) \tan (xy).
\end{align}
$$

I am under the impression the greatest difficulty is in the second partial derivative. Let's investigate in closer detail. There are two functions to be differentiated: namely $2x \tan(xy)$ and $x^2 y \sec^2 (xy)$.

The first one requires the product rule for the functions $2x$ and $\tan (xy)$, yielding $2$ and $y \sec^2 (xy)$, therefore

$$\frac{\partial}{\partial x} 2x \tan (xy) = 2 \tan (xy) + 2 xy \sec^2 (xy),$$

which are the first two terms.

The second is the hardest, because we have to apply chain rule many times: for $\sec^2 (xy)$, then for $\sec (xy)$ and then for $xy$. Differentiating $x^2 y$ gives $2xy$, but differentiating $\sec^2 (xy)$ gives

$$\frac{\partial}{\partial x} \sec^2 (xy) = 2 \sec (xy) \cdot (\tan (xy) \cdot \sec(xy)) \cdot y,$$

therefore

$$\frac{\partial}{\partial x} x^2 y \sec^2 (xy) = 2xy \sec^2 (xy) + x^2 y (2 y \sec^2 (xy) \tan(xy)) = 2xy \sec^2 (xy) + 2 (xy)^2 \sec^2 (xy) \tan (xy).$$

Best wishes. :)

 

[Yankel]

Many thanks, I found my mistake...stupid one as expected.

you mentioned the chain rule, well, I multiplied by 2, I knew that cos becomes sin (the inner function), but I forgot to multiply by cos as well...

that's what I call a big Oop's

 

[MarkFL]

thank you, can you please show me where was the mistake in my solution ?

because I just did it again for the second order derivative by y...I always get 3rd power when it's 2nd, I can't find out what I am doing wrong

I see where you are going wrong, it is in your application of the quotient rule, and within that, your application of the chain rule. It is this term you are differentiating incorrectly:

$$h(x,y)=\frac{x^2y}{\cos^2(xy)}$$

Now, applying the quotient rule to this, we find:

$$h_x(x,y)=\frac{\cos^2(xy)(2xy)-x^2y\left(2\cos(xy)\sin(xy)(y) \right)}{\cos^4(xy)}=\frac{2xy\cos(xy)-2x^2y^2\sin(xy)}{\cos^3(xy)}$$

You see, when you differentiated the term $$\cos^2(xy)$$, you wrote $$2y\sin(xy)$$, when you need $$2y\cos(xy)\sin(xy)$$. Note also that the quotient rule has a difference in the numerator, not a sum.