Partial Differential Equation: a question about boundary conditions

[Terrycho]

Homework Statement

Consider the following linear first-order PDE

Relevant Equations

Partial Differential Equations

Consider the following linear first-order PDE,

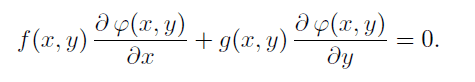
Find the solution φ(x,y) by choosing a suitable boundary condition for the case f(x,y)=y and g(x,y)=x.

---------------------------------------------------------------------------
The equation above is the PDE I have to solve and I denoted the following result by solving it.

φ(x,y)=F(t)=F(1/2 x^2 - 1/2 y^2)

So, I set the boundary condition as φ(2y, -y)=3y^2 and denoted the following result.

φ(x,y)=x^2 - y^2.

Here is my question. While I was solving the equation, I got F(t)=2t, where t=(3y^2)/2, but how do I know if this F(t) meets all the characteristic curves? Here, the characteristic curves are determined by t= x^2/2 - y^2/2 for each constant t.

 

[Orodruin]

Unless you have a particular physical situation that you want to describe ”suitable” could be any boundary condition that is compatible with the differential equation.

 

[Terrycho]

Unless you have a particular physical situation that you want to describe ”suitable” could be any boundary condition that is compatible with the differential equation.

what I heard was the boundary conditions should meet all the characteristic curves only once. Is this one wrong?

 

[Orodruin]

what I heard was the boundary conditions should meet all the characteristic curves only once.

This is correct. This specifies a single value for each characteristic curve and the rest of the values on the curves are then given by a first order ODE with that single boundary condition.

Is this one wrong?

You tell me, does the curve on which you specified the values meet each characteristic once?

 

[Terrycho]

This is correct. This specifies a single value for each characteristic curve and the rest of the values on the curves are then given by a first-order ODE with that single boundary condition.You tell me, does the curve on which you specified the values meet each characteristic once?

I mean, this is another question of mine too. φ(x,y)=F(t)=F(x^2/2 - y^2/2 ), this is the general solution of the partial differential equation irrespective of the choice of the function F. Then, I set the boundary condition as φ(2y,-y)=3y^2. While doing this, I got F(t)=2t, where t=(3y^2)/2, but how do I know if this F(t) meets all the characteristic curves? Here, the characteristic curves are determined by t= x^2/2 - y^2/2 for each constant t.

 

[pasmith]

The characteristic curves are hyperbolae with asymptotes x + y = 0 and x - y = 0. For each t \neq 0 the corresponding hyperbola consists of two disjoint continuous curves.

If you specify a boundery condition on a straight line which is not one of the asymptotes, that line will intersect each part of each characteristic exactly once, as you may verify by solving ax + by = c and x^2 - y^2 = 2t simultaneously.

 

[Terrycho]

The characteristic curves are hyperbolae with asymptotes x + y = 0 and x - y = 0. For each t \neq 0 the corresponding hyperbola consists of two disjoint continuous curves.

If you specify a boundery condition on a straight line which is not one of the asymptotes, that line will intersect each part of each characteristic exactly once, as you may verify by solving ax + by = c and x^2 - y^2 = 2t simultaneously.

So with that boundary condition I specified, F(t)=2t meets all the characteristic curves, which are the hyperbole, right?

Then how do you express F(t)=2t? Is it like y=2t, which is parallel to x-axis for each constant t?