- #1
a1234
- 77
- 6
- Homework Statement
- A second order differential equation was found to have a solution, y_2 (provided below). Apply the boundary conditions y(1) = 1 and lim of y as y approaches 0 = 0 to find the unique solution.
- Relevant Equations
- Original differential equation and obtained solution provided in the box below.
The original differential equation is:
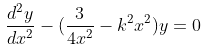
My solution is below, where C and D are constants. I have verified that it satisfies the original DE.
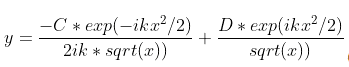
When I apply the first boundary condition, I obtain that
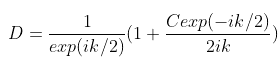 , but I'm unsure where to go from there to apply the second boundary condition. I know that I should try to choose C such that the undefined contributions from both terms cancel out, but haven't found anything that does this.
, but I'm unsure where to go from there to apply the second boundary condition. I know that I should try to choose C such that the undefined contributions from both terms cancel out, but haven't found anything that does this.
My solution is below, where C and D are constants. I have verified that it satisfies the original DE.
When I apply the first boundary condition, I obtain that