Partial Differentiation in Lagrange's Equations

[sams]

In Section 7.6 - Equivalence of Lagrange's and Newton's Equations in the Classical Dynamics of Particles and Systems book by Thornton and Marion, pages 255 and 256, introduces the following transformation from the x_i-coordinates to the generalized coordinates q_j in Equation (7.99):

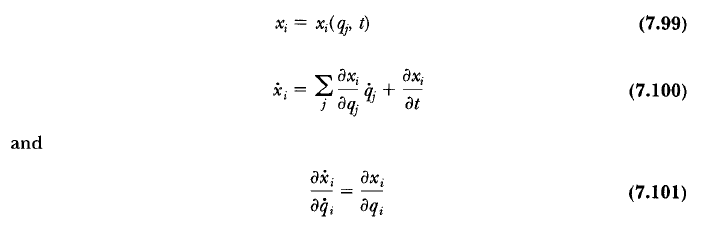
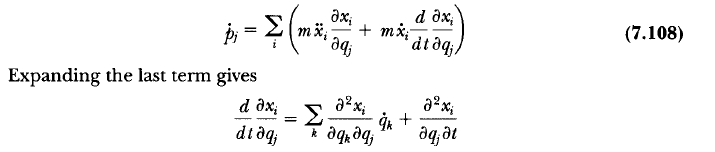
My questions are mathematical rather than physical questions.

1. Could anyone please explain to me how did the Author make the derivative of x in Equation (7.100) and expanded the time derivative of x in the last term of Equation (7.108)?

2. Is there any mathematical relation of the partial derivatives used for the above two cases?

Your help is much appreciated. Thanks a lot...

 

[kuruman]

Both situations involve application of the chain rule of differentiation.
$$\dot {x}=\frac{d}{dt}x(q,t)=\frac{\partial x}{\partial q}\frac{\partial q}{\partial t}+\frac{\partial x}{\partial t}=\frac{\partial x}{\partial q}\dot q+\frac{\partial x}{\partial t}$$

 

[sams]

Where did the second term ∂x/∂t came from?

 

[kuruman]

Where did the second term ∂x/∂t came from?

Perhaps a simple concrete example would be appropriate at this point because it looks like you are confused about what a total derivative means.
Suppose $x(q,t) = 3q^2t$ where $q=t^4$. What is $\dot x$?
Answer I (according to the rule I gave you)
$$\dot x= \frac{\partial x}{\partial q}\dot q+\frac{\partial x}{\partial t}=3 (2q)t\dot q+3q^2 =3 (2t^4)t4t^3+3t^8=27t^8$$Answer II (replacing $q=t^4$ in the original expression)
$$\dot x= \frac{d x}{dt}[3(t^8)t]=27t^8$$Clearly the answers would not match if one dropped the $\frac{\partial x}{\partial t}$ term in Answer I.

 

[Ibix]

Where did the second term ∂x/∂t came from?

The same place as the others. The chain rule says that if you have a function $f(q_1,q_2,...,q_n)$ where the $q_i$ are functions of $t$ then the derivative of $f$ with respect to $t$ is $$\frac{df}{dt}=\frac{\partial f}{\partial q_1}\frac{dq_1}{dt}+\frac{\partial f}{\partial q_2}\frac{dq_2}{dt}+...+\frac{\partial f}{\partial q_n}\frac{dq_n}{dt}$$You seem comfortable with that (I've just expanded the sum in 7.100). Now what if $q_n(t)=t$? Which is to say, what if the function $f$ has (n-1) dependencies on functions $q_j$ and one explicit dependence on $t$, as your $x_i(q_j,t)$ functions do? In that case, the last term simplifies to $\partial f/\partial t$. That's all that's going on.

 

[sams]

Thanks a lot! That was very helpful...

The second term in Equation (7.101) is not equal to zero, how did we prove this equation? Is there any certain rule in Mathematics for this relation?

 

[kuruman]

Thanks a lot! That was very helpful...

The second term in Equation (7.101) is not equal to zero, how did we prove this equation? Is there any certain rule in Mathematics for this relation?

It's the chain rule of differentiation. You must have proved it in calculus I.
If you have a function $f(u,v)$ then
$$\frac{df(u,v)}{dt}=\frac{\partial f}{\partial u}\frac{\partial u}{\partial t}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial t}$$
What do you get when $v=t$?

 

[Ibix]

The second term in Equation (7.101) is not equal to zero, how did we prove this equation? Is there any certain rule in Mathematics for this relation?

I think the point is that nothing on the RHS of 7.100 has any explicit dependence on $\dot{q_i}$ except $\dot{q_i}$ itself. So the partial derivatives of every term with respect to $\dot{q_i}$ are zero except for the one term where $j=i$, which gives you 7.101.