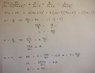SUMMARY
The forum discussion centers on solving the equation 97x + 35 = A(5x + 2)² + B(2x - 3)(5x + 2) + C(2x - 3) for the coefficients A, B, and C. The correct coefficients are A=2, B=-5, and C=1. Participants emphasize the importance of expanding the equation and equating coefficients rather than substituting values prematurely. The discussion highlights the validity of using specific x-values to eliminate terms, despite concerns about multiplying by zero at those points.
PREREQUISITES
- Understanding of algebraic manipulation and polynomial equations
- Familiarity with partial fraction decomposition
- Knowledge of the concept of equivalence in algebraic expressions
- Experience with solving systems of equations
NEXT STEPS
- Study the method of partial fraction decomposition in detail
- Learn how to expand polynomials and equate coefficients
- Explore the implications of multiplying both sides of an equation by zero
- Practice solving similar algebraic equations with varying coefficients
USEFUL FOR
Students studying algebra, mathematics educators, and anyone seeking to improve their skills in solving polynomial equations and understanding partial fractions.