Particle in a box : Schrodinger Eq

[postechsung]

Homework Statement

Particle in a box

Relevant Equations

Schrodinger Eq

Hi, I'm trying to prove a wave equation of particle in a box situation.
In many solutions, they used a equation like Eq = Asin(kx)+Bcos(kx).
Instead, I want to prove using Eq = Aexp(ikx) + Bexp(-ikx).
So, this is my solution.

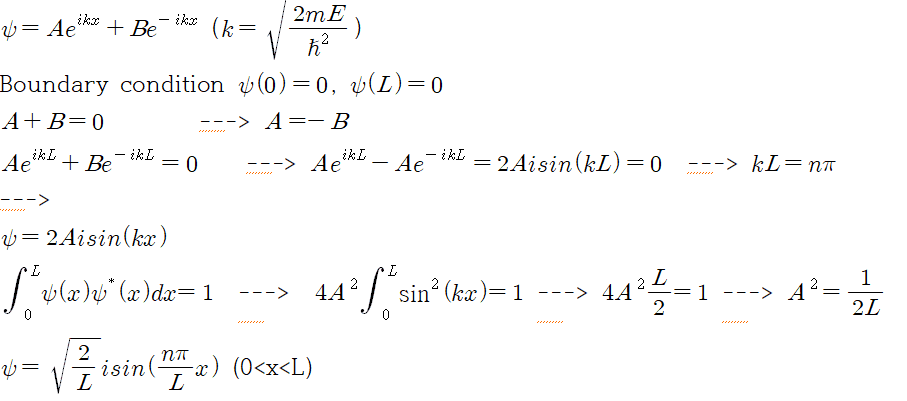
However, the original (well-known) solution is without i. (psi = sqrt(2/L) sin(n pi x/L)
Is two wave function is same? or is there any error in my solution?
Sorry for my bad English. I'm new to here and looking forward to get help.

THANKS!

 

[anuttarasammyak]

They are same. Any factor of magnitude 1 ,$e^{i\phi}$, can be multiplied to the answer.

 

[DrClaude]

However, the original (well-known) solution is without i. (psi = sqrt(2/L) sin(n pi x/L)
Is two wave function is same? or is there any error in my solution?

It's not the same wave function, but it corresponds to the same physical state. Physical states are defined up a an arbitrary complex phase $e^{i \phi}$.

 

[postechsung]

It's not the same wave function, but it corresponds to the same physical state. Physical states are defined up a an arbitrary complex phase $e^{i \phi}$.

If it's not the same wave function, does it mean there is an error in my solution?
Thanks for replying!

 

[PeroK]

If it's not the same wave function, does it mean there is an error in my solution?
Thanks for replying!

Both $\psi_n(x)$ and $i\psi_n(x)$ are normalised solutions of the equation. The mathematics cannot prefer one to the other. As the equation is linear, any solution can be expressed as a linear combination of $\psi_n(x)$ or a linear combination of $i\psi_n(x)$. These are, therefore, equally valid as a set of basis solutions (eigenfunctions).

The only reason to choose $\psi_n(x)$ (by convention) is that the $i$ is unnecessary. And, having the eigenfunctions real valued may make them slightly easier to work with.

 

[postechsung]

They are same. Any factor of magnitude 1 ,$e^{i\phi}$, can be multiplied to the answer.

It's not the same wave function, but it corresponds to the same physical state. Physical states are defined up a an arbitrary complex phase $e^{i \phi}$.

Both $\psi_n(x)$ and $i\psi_n(x)$ are normalised solutions of the equation. The mathematics cannot prefer one to the other. As the equation is linear, any solution can be expressed as a linear combination of $\psi_n(x)$ or a linear combination of $i\psi_n(x)$. These are, therefore, equally valid as a set of basis solutions (eigenfunctions).

The only reason to choose $\psi_n(x)$ (by convention) is that the $i$ is unnecessary. And, having the eigenfunctions real valued may make them slightly easier to work with.

Thanks for amazing answers for solving my question.