Particle in equilibrium (balancing forces on an object on an incline)

[Justin_Lahey]

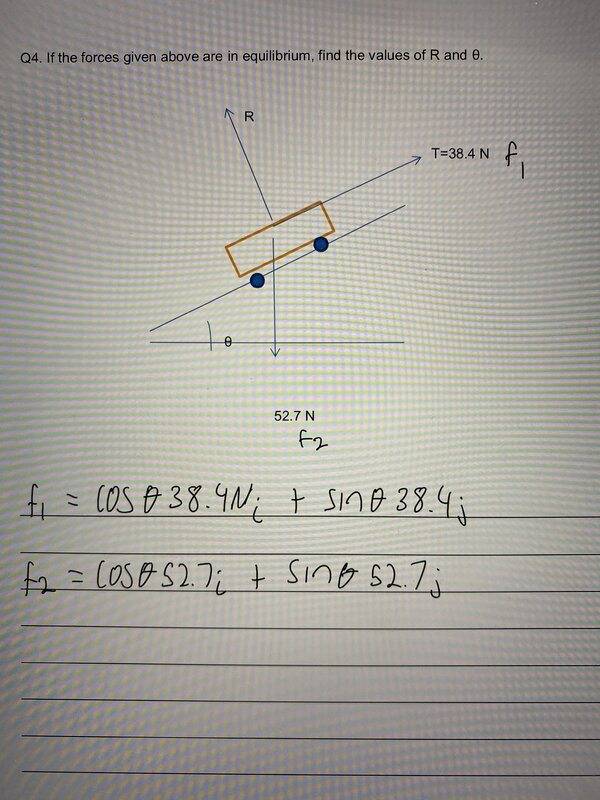
Homework Statement

Find the magnitude and angle

Relevant Equations

F1= cos(theta)38.4i+ sin(theta)38.4j
F2= cos(theta)52.7i + sin(theta)52.7j

Hi, I’m wondering if someone can help me understand this question. I can find a resultant force/vector when given an initial angle but I’m stuck here when the only information is the two magnitudes. I think I’m solving for the unknowns but a little lost on how or what equation I should be using. In the pic this is how I normally start by finding the x and y components but without theta I’m a bit lost. Thanks for any help.

 

[Mayhem]

If I am understanding the term "equilibrium" (in this context) correctly, shouldn't the net force simply be 0? So you know that F1 + F2 + R = 0.

Can you find $\theta$ from there?

 

[Delta2]

First of all you got to tell us your coordinate system. I think none of your two equations are correct (especially if we take the coordinate system with the i-direction parallel to the incline and the j direction perpendicular to the incline).

I assume you have been taught the following equation $$\vec{F}=|\vec{F}|\cos\theta\hat i+|\vec{F}|\sin\theta\hat j$$
which you apply it in a wrong way in this problem. You got to be careful what the angle $\theta$ is in this equation. It is the angle that the force vector $\vec{F}$ makes with the x-axis (or i-axis should i say, and that's why i asked what is your coordinate system). It is not the same $\theta$ for all forces (each force has its own $\theta$ in other words ) and it is not the angle $\theta$ that is given in the problem statement as the angle of the incline.

 

[haruspex]

I think none of your two equations are correct

Well, the F1 equation is right if $\hat i$ is horizontally to the right and $\hat j$ is vertically up; the F2 equation is right if $\hat i$ is normal to the slope and down to the right, and $\hat j$ is parallel to the slope and down to the left.

 

[Delta2]

Well, the F1 equation is right if $\hat i$ is horizontally to the right and $\hat j$ is vertically up; the F2 equation is right if $\hat i$ is normal to the slope and down to the right, and $\hat j$ is parallel to the slope and down to the left.

E hehe @haruspex you did some sort of reverse engineering to find coordinate systems ( you got me, i could never think of the i direction as normal to the slope, good one) that each equation is true, Still there is no single coordinate system that both simultaneously are true . Thats my main point that's why i first asked what is the coordinate system he is using.

 

[Lnewqban]

Welcome, Justin!
The way I would see this problem:
There would not be equilibrium for the case of a slope with very little θ angle, since $F_1$ would accelerate the car.
The magnitude of $F_2$ remains always the same.
As the angle of the slope increases little by little, a component of $F_2$ that is parallel to the surface of the slope an in line with $F_1$ appears and also increases little by little.

Your angle is the angle at which the magnitude of that component reaches the magnitude of $F_1$ and the balance is achieved, so the car does not accelerate in any direction.

Force R and the component of F2 that is perpendicular to the surface of the slope will naturally balance each other (Third law of Newton).