- #1
kent davidge
- 933
- 56
Homework Statement
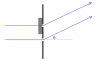
In a Young’s two-slit experiment a piece of glass with an index of refraction and a thickness is placed in front of the upper slit. (a) Describe qualitatively what happens to the interference pattern. (b) Derive an expression for the intensity of the light at points on a screen as a function of n, L and θ. Here θ is the usual angle measured from the center of the two slits. (c) From your result in part (b) derive an expression for the values of θ that locate the maxima in the interference pattern.
Homework Equations
The Attempt at a Solution
(Sorry my bad English). Let φ be the phase difference between the two waves. When φ is equal to 2π the path difference dsinθ + d2 is equal to one wavelength. I've not found a relationship between L, n and the angles of incidence and refraction. So I've considered simply that the extra distance d2 should be proportional to L and n. When n is equal to zero, the light doesn't bend and the path difference is simply dsinθ. The larger value of n, the greater distance d2. So:
2π/φ = [dsinθ + L(n - 1)] / λ
Is it a correct assumption?
See my sketch below:
Last edited: