Hello Paul,
1.) We are asked to find the equation of the tangent and normal lines to the curve $$y=\frac{x}{a}+\frac{a}{x}$$ at $$\left(\frac{a}{2},\frac{5}{2} \right)$$.
First, we need to compute the derivative of the curve to find the slopes:
$$\frac{dy}{dx}=\frac{1}{a}-\frac{a}{x^2}=\frac{x^2-a^2}{ax^2}$$
Hence, the slope of the tangent line is:
$$m=\left.\frac{dy}{dx} \right|_{x=\frac{a}{2}}=\frac{\left(\frac{a}{2} \right)^2-a^2}{a\left(\frac{a}{2} \right)^2}=-\frac{3}{a}$$
and so the slope of the normal line is:
$$-\frac{1}{m}=\frac{a}{3}$$
We now have the slopes and the point, so applying the point-slope formula, we find:
i) Tangent line:
$$y-\frac{5}{2}=-\frac{3}{a}\left(x-\frac{a}{2} \right)$$
$$y=-\frac{3}{a}x+4$$
ii) Normal line:
$$y-\frac{5}{2}=\frac{a}{3}\left(x-\frac{a}{2} \right)$$
$$y=\frac{a}{3}x+\frac{15-a^2}{6}$$
Here are some plots with a few values for $a$:
https://www.physicsforums.com/attachments/814._xfImport
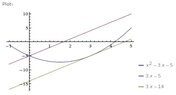
2.) We are asked to find at what point of the parabola $y=x^2-3x-5$ is the tangent line parallel to $3x-y=2$? Find the equation of the tangent line.
First we observe that we may arrange the given line in slope-intercept form as follows:
$$y=3x-2$$
Now, we want to equate the derivative of the parabola to the slope of the line (since parallel lines have equal slopes):
$$2x-3=3$$
$$x=3$$
Now, to find the $y$-coordinate:
$$y(3)=(3)^2-3(3)-5=-5$$
and so we now have the slope $$m=3$$ and the point $$(3,-5)$$, and applying the point-slope formula, we find then that the equation of the tangent line parallel to the given line is:
$$y-(-5)=3(x-3)$$
$$y=3x-14$$
Here is a plot of the parabola, the given line, and the line tangent to the parabola and parallel to the given line:
https://www.physicsforums.com/attachments/815._xfImport
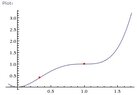
3.) We are asked to find the equation of the line normal to the curve $y=3x^5+10x^3+15x+1$ at its point of inflection.
From the first derivative, we may determine the slope of the tangent line, once we know where the point of inflection is.
$$\frac{dy}{dx}=15x^4+30x^2+15=15\left(x^2+1 \right)^2$$
$$\frac{d^2y}{dx^2}=60x^3+60x=60x\left(x^2+1 \right)=0$$
We find that the second derivative has only the real root $x=0$ and since it is of multiplicity 1, we know the second derivative changes sign across this root, hence the point of inflection is at $$(0,1)$$. Now the slope of the normal line is:
$$m=-\frac{1}{15}$$ and so, applying the point slope formula, we find the normal line is:
$$y-1=-\frac{1}{15}(x-0)$$
$$y=-\frac{1}{15}x+1$$
4.) We are asked to find the critical points and the points of inflection of the curve $y=3x^4-8x^3+6x^2$.
Critical or stationary points:
We want to equate the first derivative to zero, and solve for $x$:
$$\frac{dy}{dx}=12x^3-24x^2+12x=12x(x-1)^2=0$$
The critical values are then:
$$x=0,\,1$$
Because the root $x=1$ is of multiplcity 2, we may conclude that this is not an extremum, and by the first derivative test we know the critical value $x=0$ is at a relative minimum. Thus $$(0,0)$$ is a relative minimum.
Points of inflection:
$$\frac{d^2y}{dx^2}=36x^2-48x+12=12\left(3x^2-4x+1 \right)=12(3x-1)(x-1)=0$$
Since the roots are of multiplcity 1, we know the sign of the second derivative changes across then, and so we may conclude that the points of inflection are at:
$$\left(\frac{1}{3},\frac{11}{27} \right)$$
$$(1,1)$$
Here is a plot of the quartic function, showing its minimum at the origin and the points of inflection:
https://www.physicsforums.com/attachments/816._xfImport
To Paul and any other guests viewing this topic, I invite and encourage you to post other calculus problems here in our http://www.mathhelpboards.com/f10/ forum.
Best Regards,
Mark.
