SUMMARY
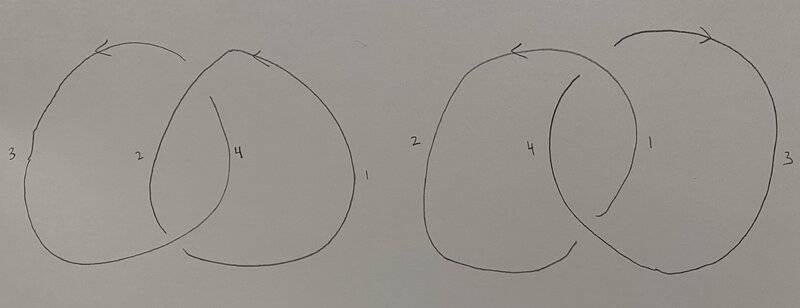
The PD code [(2, 3, 1, 4), (4, 1, 3, 2)] corresponds to a unique link diagram, specifically a Hopf link, rather than a knot diagram. The discussion clarifies that while a PD code can yield multiple link diagrams, it does not produce multiple knot diagrams. The confusion arises from the visual similarity of the diagrams, which appear as interconnected rings, leading to the misconception that they represent knots. The Hopf link consists of two linked unknots, confirming its validity as a link diagram.
PREREQUISITES
- Understanding of PD (Plane Diagram) codes
- Familiarity with knot theory terminology
- Knowledge of link diagrams versus knot diagrams
- Basic concepts of topology related to knots and links
NEXT STEPS
- Study the properties of Hopf links in knot theory
- Explore the implications of PD codes in knot and link diagrams
- Learn about the classification of knots using the Rolfsen Knot Table
- Investigate the relationship between unknots and linked structures in topology
USEFUL FOR
Mathematicians, knot theorists, and topology enthusiasts interested in the distinctions between knots and links, as well as those studying the applications of PD codes in knot diagrams.