Knot theory: closed loops in n dimensions

[DaveC426913]

I'm not a math machine, but I dabble in dimensional stuff. I think this falls under knot theory.

I have built several prototypes of a tesseract. Each of them sits in a little case in my office. One of them is made from truncated cubes, held together with elastic cord:

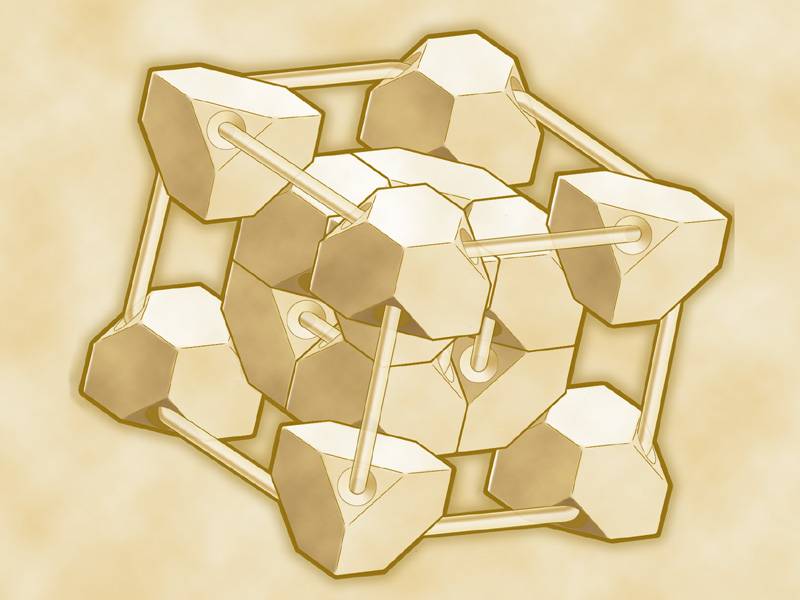
In theory, the structure I've built is transformable through all permutations (any of its eight cubes can be rotated to the centre), thus:

...in practice, there is way too much friction. (So I've moved on to a version 4 and now a version 5.)

But I learned something about this shape as I was building it. Not only does there need to be only a single elastic cord to tie it all together, but it is a continuous loop.

This became obvious only after-the-fact, when I realized the vertices (all of which are identical) have an even number of edges (four) leading to them, which means there need be (and is) no start and end point.

(I used to play with this puzzle:

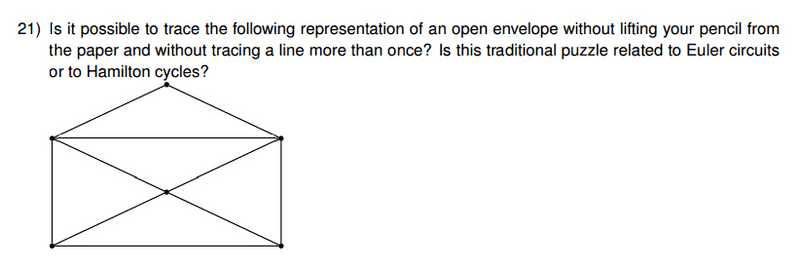
Yes, but it is not closed loop. All but two vertices have an even number of lines, so those two must form the two termini of the line.)To my question:

I want to determine if it is possible - or impossible - for the path of the elastic cord to be symmetrical i.e. so that, no matter how I permute it, I cannot distinguish one orientation from another. (I don't mean rotational in 3-D space, I mean rotate it 4D space i.e. turn it inside out, so that some other cube is at the centre.)

Other than diagramming at random, to find a solution, I have no way of solving it.

I've tried flattening it, but that doesn't get me any closer to a solution.

 

[mfb]

I'm not sure what exactly you count as distinguishable, but unless I made a mistake I can prove that at least some vertices have to be different in some way.

You have 32 edges. A circular path will pass through all 16 vertices exactly twice. We can label the vertices as A,B,...,P and write the path as list of vertices, e.g. ABCDAE... where every vertex appears twice and one connection is between the outermost letters.
For every vertex, we can measure the number of connections we have to cross until we get back to that letter. We get two even numbers with a sum of 32. I'll show that these numbers cannot be the same for every vertex.

Let's consider vertex A.
The two positions could be 16 letters apart (so both sides are 16 connections long). Let A be next to B in one place. Then B has to be next to A at the other place as well, and we have the AB connection twice -> contradiction.
The two positions could be n<16 letters and 32-n>16 letters apart. Then we get a string ABCDE...A with n different letters in it. B cannot be added to the right, so we need B..ABCDE..A. I'll call this "go backward". C has to "go forward": B..ABCDE..A_C. D has to go backward again.
If n=4, we put D next to A again, contradiction. Same problem for n=6 with F and so on. You don't find a place for the last letter before A without making a connection twice.

 

[DaveC426913]

I'm not sure what exactly you count as distinguishable, but unless I made a mistake I can prove that at least some vertices have to be different in some way.

Yes, there's won't be complete symmetry, by any means. But I can't seem to find any.

Let A be next to B in one place. Then B has to be next to A at the other place as well, and we have the AB connection twice -> contradiction.

You lost me here. What do you mean "B has to be next to A at the other place as well"?Do you think that writing out a list of 24 vertices in alphabetic form is a more fruitful way of exploring the symmetry than a visual diagram? That might be something I could try.

 

[mfb]

What do you mean "B has to be next to A at the other place as well"?

AB[15 other vertices]AB.

Do you think that writing out a list of 24 vertices in alphabetic form is a more fruitful way of exploring the symmetry than a visual diagram? That might be something I could try.

It helped with my proof.
Note that I didn't use any information about which vertices actually have connections apart from "every circle has even length" and "no pair of vertices is connected more than once".

Any symmetry? I can do that.

Spoiler: 4D coordinates

0	0	0	0
1	0	0	0
1	1	0	0
0	1	0	0
0	1	1	0
0	0	1	0
1	0	1	0
1	1	1	0
1	1	1	1
0	1	1	1
0	0	1	1
1	0	1	1
1	0	0	1
1	1	0	1
0	1	0	1
0	0	0	1
0	0	0	0
0	1	0	0
0	1	0	1
0	1	1	1
0	1	1	0
1	1	1	0
1	1	0	0
1	1	0	1
1	1	1	1
1	0	1	1
1	0	1	0
1	0	0	0
1	0	0	1
0	0	0	1
0	0	1	1
0	0	1	0
0	0	0	0

Spoiler: only the changes

0	0	0	0
1			
	1		
0			
		1	
	0		
1			
	1		
			1
0			
	0		
1			
		0	
	1		
0			
	0		
			0
	1		
			1
		1	
			0
1			
		0	
			1
		1	
	0		
			0
		0	
			1
0			
		1	
			0
		0

The path makes a "C" shape in the first two dimensions before following a single connection in one of the other dimensions to make a C shape in the first two dimensions again. After 4 iterations we are back at the starting point. At this time 3/4 of the connections in the first two dimensions and 1/4 of the connections in the other two are used. The path now does "C" shapes in the other two dimensions with single connections in the first two dimensions in between.