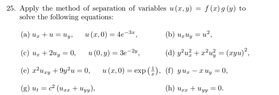Homework Help Overview
The discussion revolves around applying the method of separation of variables to solve a partial differential equation (PDE), specifically in the context of the heat equation. Participants are exploring the implications of assuming certain variables are independent and how to properly set up the separation of variables.
Discussion Character
- Exploratory, Assumption checking, Problem interpretation
Approaches and Questions Raised
- Participants discuss the substitution of variables in the PDE and question the validity of setting ##u_{t}=0##. There are suggestions to separate the variables differently, considering functions of time and space. Some participants express confusion over the problem's presentation and its implications.
Discussion Status
The discussion is ongoing, with participants providing alternative perspectives on how to approach the problem. Some suggest reconsidering the assumption of ##u_{t}=0##, while others point out potential confusion in the problem's wording. No consensus has been reached, but various interpretations are being explored.
Contextual Notes
Participants note that the problem is presented in a way that may lead to misunderstandings regarding the separation of variables. There is mention of specific exercises from a textbook, indicating that the context may be influenced by the way the question is framed.