Pendulum, electic field, equilibrium

[pompey]

Homework Statement

(This is from Giancoli 5th ed book, pg 500 problem 49)
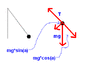
A point charge m=1.0g at the end of an insulating string 50cm long is in equilibrium in a uniform electrical field E=9200 N/C, when the pendulum is 1.0cm high. If the field point to the right, what is the magnitude of the point charge?

Homework Equations

F=Eq

The Attempt at a Solution

I think the solution is q = tan(theta)*m*g/E
where theta = arccos(.49/.50) and m=1.0g and g = 9.8m/s^2

However, I found it to be q = cos(theta)*sin(theta)*m*g/E, which I know to be wrong.

I've had trouble with free force diagrams for pendulums, and I can draw one out but I can't find the force component in the X direction. If T = tension in the string, then the component in the X direction should be sin(theta)*T. T should equal m*g*cos(theta), so shouldn't the total force in the X direction be sin(theta)*cos(theta)*m*g

 

[Mindscrape]

You're going to have to treat this as a vector problem. On one hand there is a gravitational field acting on the mass with a force vector, and on the other there is an electric field acting on a point charge with another force vector. Since all you care about is the magnitude, just arbitrarily assign a positive or negative value to the point charge for visualization purposes (it will all work out the same).

Draw out the two forces, and hopefully the relation will become apparent.

 

[turdferguson]

I've had trouble with free force diagrams for pendulums, and I can draw one out but I can't find the force component in the X direction. If T = tension in the string, then the component in the X direction should be sin(theta)*T. T should equal m*g*cos(theta), so shouldn't the total force in the X direction be sin(theta)*cos(theta)*m*g

You sure about that? Draw out a free body diagram. Tcostheta = mg, then everything should work out

 

[Mindscrape]

Or just note that, depending on what angle you solve for, tan(theta)=F_g/F_E.

 

[pompey]

I understand now that I was wrong, and I know what a free body diagram looks like. But I don't understand why.

With a = theta:
In my diagram, vector addition of mg*cos(a) and mg*sin(a) would equal mg and mg*cos(a) would equal T. Is this diagram only for a swinging pendulum without any external force?

What is the reasoning for the diagram with the external electrical force? Why does the first diagram not work?

 

[turdferguson]

Your diagram is still pending, but it sounds like you chose axes that line up with tension because weight is split up into components. Youre making much more work for yourself because the weight and electric forces are perpendicular. If you choose axes along these forces, tension is the only thing split up into components.
This problem can be solved just like a simple statics problem in which a mass is held by one horizontal and one angled string. Weight cancels the vertical component of tension and electric force cancels the horizontal component of tension. Then just divide by the field to get the charge

 

[maverick280857]

Your second diagram looks correct, except for one thing: you haven't shown the electric force on the charge. For the charge to be in equilibrium,

\vec{T} + \vec{W} + \vec{F_{elec}} = 0

You have resolved the weight correctly. The electric force on the charge is very much a "real" force that needs to be considered while computing the net force on the charge (as you already know).

As for the freebody diagram, it is helpful to indicate the angle \theta between the weight vector and the direction along the rope, until you are sufficiently proficient to resolve forces by inspection.

You see, there are three forces on the charge (particle) which must be such that their vector sum cancels (for equilibrium).

In the present system,

T\cos\theta = mg
T\sin\theta = F_{elec} = qE

Eliminate the tension force T between these two equations and that gives you your answer.

Hope that helps.