Pendulum Problem: Find Min Release Angle to Clear Peg

[dkoppes]

Homework Statement

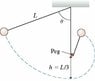
A pendulum is formed from a small ball of mass m on a string of length L. As the figure shows, a peg is height h = L/3 above the pendulum's lowest point.

From what minimum angle must the pendulum be released in order for the ball to go over the top of the peg without the string going slack?

Homework Equations

The Attempt at a Solution

I attempted to calculate the potential energy that the ball starts with at when it is released using PE = (L-L*cos(theta))*m*g and then using the potential energy at the top of the swing around the peg PE = 2/3*L*m*g and then setting them equal to each other find theta. I also tried a couple different methods that we basically just stabs in the dark and these that I just gave are the only ones that make sense. So far I have tried theta = 48.2, 70.5, and 19.5 but it says that all of these are wrong. Please help me.

 

[Doc Al]

Start by asking yourself how fast must the ball be going at the top of its motion to keep the string taut. (Hint: Use Newton's 2nd law.)

 

[dkoppes]

I did try that, but I still couldn't figure it out, that was one of the methods that I tried.

 

[EP]

Show us what you exactly tried, with respect to Doc Al's advice.

 

[tim_lou]

first, find out the tension of the rope at the top as a function of angle. What is the relationship between the tension and gravity? what is the net force? What happens when the tension is zero?

 

[crcrzy12]

for the rope to not have any slack in it, doesn't tension have to = m*g

 

[EP]

At what point are you considering?

 

[turdferguson]

So once you have centripetal acceleration, find the minimum velocity at the top of the swing. At the top of the swing, how much how much potential energy does the ball have? How much higher does the ball have to start out? You were on the right track before, but you have to factor in the minimum kinetic energy, its not zero

 

[Mwhit]

Remember that you have to account for the kinetic AND the potential energy of the ball after it hits the peg and swings around.

So...

PE = KE + PE

 

[Gianna_07]

Im also having trouble with this problem.

I first solved for the critical velocity (when the force normal = 0) and got sqrt(g*L/3).
I then used the conservation of energy equation,
1/2(m)(vf)^2+(m)(g)(yf)=1/2(m)(vi)^2+(m)(g)(yi)
Since vi = 0, and the masses cancel, I was left with
1/2(vf)^2+(m)(g)(yf) =(g)(yi)

I then solved for v:

(vf)^2=2(gyf-gyi)

so

(L/3)g = 2(L-Lcos(theta))-2(L/3)

substituting the critical velocity for vf and factoring out the L and g, I solved for theta and got 60 degrees.

Can anyone please see where I'm going wrong?

Thanks!

 

[Gianna_07]

never mind, wrong equation! thanks

 

[kramerbaggins]

I am having trouble with this one. Which equation was wrong?