Penrose Diagrams - Introduction

[Jolb]

Penrose Diagrams -- Introduction

I'm woefully ignorant of a lot of things in GR, and now that I'm moving away from my comfortable spot in condensed matter, I'd like to know how to interpret Penrose diagrams. I'm having trouble understanding what it is they're actually showing and why they'd be useful. For example, take a look at this diagram:

Why is it useful to squish down the geometry of spacetime so that infinity is on the edges? What significance does it have to cross from the lower diamond to the top left triangle, other than that now you're inside the event horizon?

Is the diagram showing us that the horizon is a coordinate singularity, and that's why it would be located toward the future at infinity? Is this also showing that the event horizon becomes light-like when viewed from some particular reference frame? At the point where the horizon and "anti-horizon" come together, does this indicate the black hole is born at that event?

I'm really looking for any kind of helpful introduction. I'm pretty lost and any tips or references would be greatly appreciated!

 

[WannabeNewton]

The "squishing" part is a conformal isometric embedding of space-time into an open subset of a compact topological space so that by suppressing unneeded dimensions, we can represent the entirety of space-time on a 2D diagram and characterize its causal structure diagrammatically. It is not unlike the various compactification of topological spaces e.g. Alexandroff compactification in which we construct a new topological space based on a given locally compact Hausdorff space by including the points at infinity and define a topology which makes the new space compact and the original space a dense embedding in the new space. We can use this to make the Riemann sphere the Alexandroff compactification of the complex plane; the Riemann sphere is homeomorphic to $S^{2}$ so that should give you an intuition for what's going on. What is being done with conformal diagrams is similar except we are considering isometric embeddings as opposed to just topological embeddings.

For an informal summary: http://jila.colorado.edu/~ajsh/insidebh/penrose.html
For something a bit more detailed: http://www.ift.uni.wroc.pl/~blaschke/master/Felinska.pdf
http://www.phy.syr.edu/courses/PHY312.00Spring/notes/lecnotes/lec24.pdf
See also appendix H of Carroll's GR text.

EDIT: Also see here: http://ls.poly.edu/~jbain/philrel/philrellectures/14.BlackHoles2.pdf

 

[PeterDonis]

I'd like to know how to interpret Penrose diagrams. I'm having trouble understanding what it is they're actually showing and why they'd be useful.

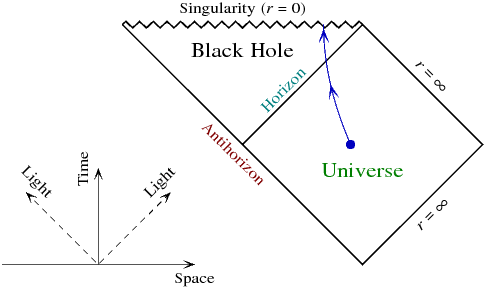
Two key advantages of Penrose diagrams are that they show causal structure easily (i.e., which parts of the spacetime can send or receive causal influences to or from which other parts of the spacetime), and that they make the conformal structure of the spacetime obvious (i.e., what kinds of "infinity" are in the spacetime and how they are structured).

Why is it useful to squish down the geometry of spacetime so that infinity is on the edges?

Because there are different kinds of "infinity" that a spacetime can have, and it's useful to know which kinds a particular spacetime has.

For example, consider the diamond labeled "Universe" in the diagram you gave. The right corner of the diamond is called "spacelike infinity" or $i^0$; the two 45 degree lines on the right (labeled r = infinity) are called "future null infinity" (the upper one), or $\mathscr{I}^+$, and "past null infinity" (the lower one), or $\mathscr{I}^-$, and the top and bottom corners are called "future timelike infinity" (the top one), or $i^+$, and "past timelike infinity" (the bottom one), or $i^-$. The diagram tells us some key things about these infinities:

$i^0$ is a single point: that means all spacelike lines that go to infinity (a spacelike line can be thought of as a "line of constant time") all meet at a single point at infinity. There are some spacetimes that don't have a spacelike infinity at all, so the diagram is useful in telling us that this isn't one of them.

$i^+$ and $i^-$ are also single points: that means all timelike lines (i.e., all possible worldlines of ordinary objects with nonzero rest mass) converge in the infinite past and the infinite future. There are spacetimes which do not have future and/or past timelike infinities, but instead have something else there, such as a singularity (not to be confused with the black hole singularity in this spacetime); again, the diagram is useful in telling us what we are dealing with.

$\mathscr{I}^+$ and $\mathscr{I}^-$ are not points, but lines; this indicates that light rays coming in from the infinite past, and light rays going out to the infinite future, (a) do *not* go to or come from "the same place" as spacelike lines or timelike lines, which is important in itself; and (b) do not all go to or come from "the same place" even among themselves--different light rays go to or come from different points at infinity. This allows us to label light rays according to which particular point at infinity they go to or come from, which can be useful.

What significance does it have to cross from the lower diamond to the top left triangle, other than that now you're inside the event horizon?

Notice that the event horizon itself is a 45-degree line. 45-degree lines in Penrose diagrams are causal boundaries--in this case, the horizon is the boundary of a region of spacetime, the black hole, that cannot send causal signals to future infinity (null and timelike). The Penrose diagram makes this obvious: no point in the upper left triangle can be connected by a causal line (45 degrees upward or more vertical than that) to any point in the "Universe" diamond or its boundaries at infinity.

This also shows another reason why squishing down the geometry so infinity is brought into a finite point is useful: if you didn't do that, it would be harder to tell whether or not a particular point can be connected to infinity by a causal line. With infinity at a finite point on the diagram, it's simple.

Is the diagram showing us that the horizon is a coordinate singularity

No. Being a coordinate singularity depends on the coordinates you use. The horizon is not a coordinate singularity in Penrose coordinates (the ones used to draw the diagram).

and that's why it would be located toward the future at infinity?

The horizon is not at infinity; it's not on a boundary of the diagram. One key thing that the diagram doesn't communicate well: the horizon doesn't actually connect to $i^+$ (the top point of the "Universe" diamond); that connection is blocked by the singularity at the top of the diagram.

Is this also showing that the event horizon becomes light-like when viewed from some reference frame accellerated such that it doesn't fall into the singularity?

The event horizon is lightlike in any reference frame; being lightlike is an invariant property and is not frame-dependent. However, it is true that the fact of the horizon being lightlike can be easily read off from a Penrose diagram, unlike some other coordinate diagrams: the horizon is a 45-degree line.

 

[WannabeNewton]

Is this also showing that the event horizon becomes light-like when viewed from some particular reference frame?

A hypersurface $\Sigma\subset M$ specified by $\varphi(x^{a}) = \text{const.}$, where $\varphi\in C^{\infty}(M)$, is null if the normal vector field $\nabla^{a} \varphi$ is null on $\Sigma$. As you can see, this is a geometric property of $\nabla^{a} \varphi$ i.e. coordinate/frame independent. We say that the integral curves of $\nabla^{a} \varphi$ contained in $\Sigma$, which will necessarily be null geodesics, are the null geodesic generators of $\Sigma$.

 

[Jolb]

Thanks Wannabe and Peter! Peter's answers to my questions were very helpful, and I appreciate you pointing out the subtleties that aren't obvious just from the diagram. Of course I should have remembered that if something is light-like in one frame it is light-like in all frames (no fancy math needed, Wannabe), but that really strikes me as an odd fact (being a newbie to GR) since I would assume it's possible to be in a frame where the event horizon is "stationary" just like the surface of a star.

Anyway, it seems to me like the diagrams aren't that complicated, they're more-or-less a warped Minkowki diagram on which you can represent all the counterintuitive things that people know of from GR (and those are what's confusing me).

 

[PeterDonis]

I would assume it's possible to be in a frame where the event horizon is "stationary" just like the surface of a star.

It isn't, for the same reason it isn't possible to be in a frame where a light beam is stationary. That's what "lightlike" means.

Don't be misled by the fact that the event horizon has a fixed $r$ coordinate; that's one of those counterintuitive subtleties. Our normal intuition is to think of the $r$ coordinate as a spatial coordinate, a "radius", something that labels "points in space"; but that is only true outside the horizon.

 

[Jolb]

Thanks for the further clarification, Peter!

That's what "lightlike" means.

Of course. Had I been more careful to write what I actually meant instead of the dumb thing I actually wrote, I would have said:

Of course I should have remembered that if something is light-like in one frame it is light-like in all frames (no fancy math needed, Wannabe), but the fact that the horizon is light-like really strikes me as an odd fact (being a newbie to GR) since I would assume it's possible to be in a frame where the event horizon is "stationary" just like the surface of a star.

Anyway, you read my mind before I could clarify:

Don't be misled by the fact that the event horizon has a fixed $r$ coordinate; that's one of those counterintuitive subtleties. Our normal intuition is to think of the $r$ coordinate as a spatial coordinate, a "radius", something that labels "points in space"; but that is only true outside the horizon.

That is precisely what I find so odd. I guess I just need to read further into my copy of D'Inverno before this makes sense to me.

 

[maxverywell]

I have difficulty in understanding the Penrose diagram for a spherically symetric collapse of a star that forms the Schwarzschild BH. It seems very confusing to me.

Here's the diagram:

My questions about this diagram are:

1) Why the Schwarzschild radius (orange curve) and the event horizon (green line) are different? It seems that after the yellow line (the surface of the star) crosses the orange line (the Schwarzschild radius), the light from the surface of the star can still escape to the future lightlike infinity because it haven't crossed the event horizon yet.

2) Is the region in the left to the yellow curve the star's interior?

3) Why the r=0 is drawn both as a vertical line and as a horizontal line (singularity)?

 

[PeterDonis]

1) Why the Schwarzschild radius (orange curve) and the event horizon (green line) are different?

I can't say because I'm not sure what the orange curve is supposed to represent; other Penrose diagrams that I've seen of this scenario don't have the orange line, and the term "Schwarzschild radius" doesn't make sense in describing it, for the reason you give. Can you give a link to the website where you got this diagram?

2) Is the region in the left to the yellow curve the star's interior?

Yes.

3) Why the r=0 is drawn both as a vertical line and as a horizontal line (singularity)?

Because it is both. That's one of the counterintuitive things about this spacetime. r = 0 starts out as a spatial location, the center of the collapsing object, a non-singular spatial location. But when the collapse is complete, r = 0 turns into a singularity, and it's a spacelike singularity--it's not a location in space, but a moment of time, which is in the future of any event inside the horizon. That's why it becomes horizontal; the change from vertical to horizontal is the change from nonsingular spatial location to spacelike singularity.

 

[DrGreg]

I can't say because I'm not sure what the orange curve is supposed to represent; other Penrose diagrams that I've seen of this scenario don't have the orange line, and the term "Schwarzschild radius" doesn't make sense in describing it, for the reason you give.

I agree. I would guess that maybe the orange line is supposed to be a line of constant r coordinate, in Schwarzschild coordinates, outside the event horizon.

 

[maxverywell]

Thnx Peter!
I found the diagram here http://motls.blogspot.gr/2008/11/why-can-anything-ever-fall-into-black.html

But I have seen it also in other places

Also here, on page 47: http://arxiv.org/pdf/gr-qc/9707012v1.pdf
(Black Holes, Lecture notes by Dr. P.K. Townsend, DAMTP, University of Cambridge)

No one really explains what it is...

 

[maxverywell]

I have another question. How the lightlike geodesics get from $\mathcal{I}^{-}$ to $\mathcal{I}^{+}$ in this diagram (those that don't cross the horizon)? Do they "reflect" at the vertical line (r=0) and then move at $45^{\circ}$ to the $\mathcal{I}^{+}$?

 

[DrGreg]

I found the diagram here http://motls.blogspot.gr/2008/11/why-can-anything-ever-fall-into-black.html

Hmm. the description there initially describes the orange line as "the points where the radius of the internal sphere is "R=2GM/c^2"", but later (in the section "The orange observer") refers to a "spaceship ... at "r=const" in Schwarzschild coordinates where "const" is just a little bit higher than the Schwarzschild radius, "r=2GM/c^2""

Also here, on page 47: http://arxiv.org/pdf/gr-qc/9707012v1.pdf
(Black Holes, Lecture notes by Dr. P.K. Townsend, DAMTP, University of Cambridge)

That diagram has nothing labelled "horizon" on it, so it doesn't really help resolve the original diagram.

 

[maxverywell]

That diagram has nothing labelled "horizon" on it, so it doesn't really help resolve the original diagram.

But that diagram has the curve r=2GM which is drawn as timelike curve and ends at $i^{+}$. Doesn't make sense. Horizon is a null line.

 

[PeterDonis]

I have another question. How the lightlike geodesics get from $\mathcal{I}^{-}$ to $\mathcal{I}^{+}$ in this diagram (those that don't cross the horizon)? Do they "reflect" at the vertical line (r=0) and then move at $45^{\circ}$ to the $\mathcal{I}^{+}$?

Yes. This just means that the light ray passes through the center and goes out in the opposite direction. One thing to keep in mind is that each point in the Penrose diagram is actually a 2-sphere (except the points at r = 0), because the angular coordinates are suppressed.

 

[PeterDonis]

I found the diagram here http://motls.blogspot.gr/2008/11/why-can-anything-ever-fall-into-black.html

Also here, on page 47: http://arxiv.org/pdf/gr-qc/9707012v1.pdf
(Black Holes, Lecture notes by Dr. P.K. Townsend, DAMTP, University of Cambridge)

Looking at these two, I think the confusion is that the $r = 2M$ line looks different inside the collapsing matter, and the horizon itself is at $r < 2M$ inside the collapsing matter. At some point during the collapse, the horizon forms at $r = 0$ and moves outwards; it reaches $r = 2M$ at the exact instant that the surface of the collapsing matter passes through that radius on its way inward. After that, the horizon stays at $r = 2M$.

Therefore, if we follow the curve $r = 2M$ from $i^-$ on, it will be inside the collapsing matter until the instant that the surface of the collapsing matter reaches $r = 2M$, and the horizon reaches there as well, at the same instant.

In Motl's diagram, as DrGreg noted, I think the orange line can't be at $r = 2M$; it must be slightly higher, because, as you point out, it ends at $i^+$.

In Townsend's diagram, as DrGreg noted, there is no "horizon" line; but if the line labeled $r = 2M$ really is at that $r$ coordinate, then the portion of that line that is outside (i.e., to the right of) the collapsing matter must actually be the portion of the horizon that is outside the collapsing matter; i.e., it is not intended to intersect $i^+$, but to go up and to the right at 45 degrees until it hits the rightmost end of the singularity at $r = 0$.

So if we superimposed Townsend's and Motl's diagrams, Motl's orange line would lie slightly outside (i.e., to the right of) Townsend's $r = 2M$ line.