HansBu
- 24
- 5
- Homework Statement
- I have a problem involving the new chaotic system dubbed as the Chen System. This involves a system of coupled nonlinear ordinary differential equations. My problem is to determine for which parameters a, b, and c would yield a periodic and chaotic solution.
- Relevant Equations
- The relevant equations are posted in the section below.
Here is the Chen System
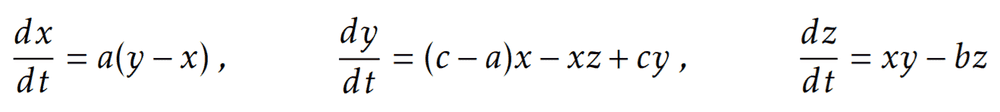
I am given the initial condition (t=0) that a particle lies on the xyz-plane at a point (-10,0,35). I was notified that if I plugged in a=40, b=5, and c=30, the trajectory of the particle will be chaotic. On the other hand, if I retained the values of a and c, and changing b to b = 10, periodic solutions will be obtained. My concern relies on how were these values picked. Is there any sort of mathematics (analytically) that was used here? I would appreciate any help that you would render. Below is the graph for the chaotic path of the particle.
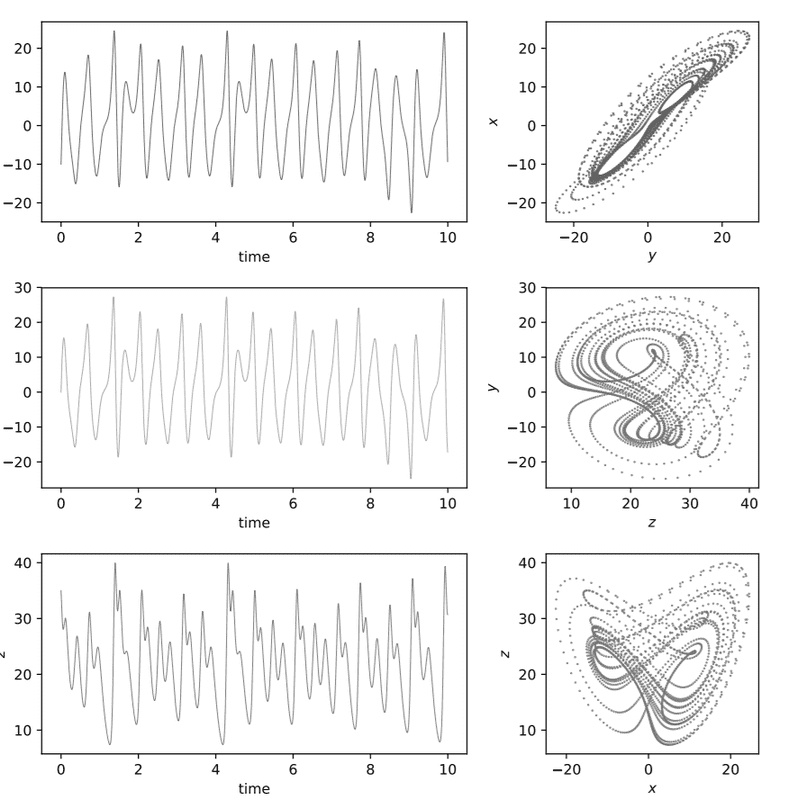
I am given the initial condition (t=0) that a particle lies on the xyz-plane at a point (-10,0,35). I was notified that if I plugged in a=40, b=5, and c=30, the trajectory of the particle will be chaotic. On the other hand, if I retained the values of a and c, and changing b to b = 10, periodic solutions will be obtained. My concern relies on how were these values picked. Is there any sort of mathematics (analytically) that was used here? I would appreciate any help that you would render. Below is the graph for the chaotic path of the particle.