pinsky
- 95
- 0
Hy
I'm having some issues about the Newtons third law.
The image should represent a person in a bus with and the forces acting on them.
The bus and the person are observed from outside the bus. The bus starts accelerating because of the force F_{BUS MOVING}. This force represent the resultant force of the friction between the bus and the ground, and the buses starting force.
As a result, friction force F_{P-BUS} occurs and it acts on the bus because of the mass of the person.
As a reaction, a force of the same size but opposite direction acts on the person F_{BUS-P}
What is the sum of the forces on the bus?
F_{BUS MOVING}-F_{P-BUS} ?
How would one calculate F_{P-BUS} by knowing the mass of the person and \mu?
Is this the solution?
F_{BUS MOVING}-F_{P-BUS}=F_{BUS-P}
Since in this case, the bus and the person have the same value and orientation. That is what a observer from the street would see, right?
I'm having some issues about the Newtons third law.
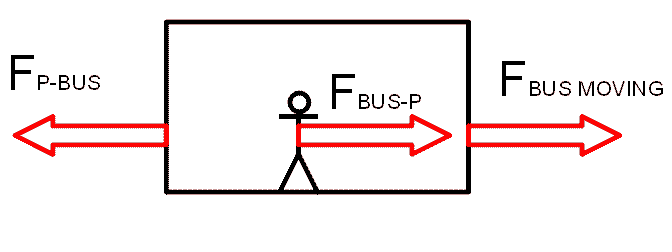
The image should represent a person in a bus with and the forces acting on them.
The bus and the person are observed from outside the bus. The bus starts accelerating because of the force F_{BUS MOVING}. This force represent the resultant force of the friction between the bus and the ground, and the buses starting force.
As a result, friction force F_{P-BUS} occurs and it acts on the bus because of the mass of the person.
As a reaction, a force of the same size but opposite direction acts on the person F_{BUS-P}
What is the sum of the forces on the bus?
F_{BUS MOVING}-F_{P-BUS} ?
How would one calculate F_{P-BUS} by knowing the mass of the person and \mu?
Is this the solution?
F_{BUS MOVING}-F_{P-BUS}=F_{BUS-P}
Since in this case, the bus and the person have the same value and orientation. That is what a observer from the street would see, right?
Attachments
Last edited: