SUMMARY
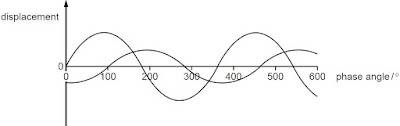
The phase difference between two light waves of the same frequency can be represented in multiple ways. In this discussion, a phase difference of 100º was initially identified, but the correct answer is 260º. This discrepancy arises from the choice of reference wave; either wave can be considered the starting point. The mathematical representation of the waves is given by the functions ##\sin(\theta+\phi_1)## and ##\sin(\theta+\phi_2)##, where the phase difference is calculated as ##\phi_2 - \phi_1## or ##\phi_1 + 2\pi - \phi_2##.
PREREQUISITES
- Understanding of wave functions and their graphical representations
- Knowledge of phase difference in wave mechanics
- Familiarity with trigonometric functions, specifically sine
- Basic concepts of angular measurement in degrees
NEXT STEPS
- Study the concept of phase difference in wave mechanics
- Learn how to graphically represent wave functions using tools like Desmos or MATLAB
- Explore the mathematical properties of sine functions and their phase shifts
- Investigate the implications of choosing different reference points in wave analysis
USEFUL FOR
Students and professionals in physics, particularly those focused on wave mechanics, as well as educators looking to explain phase differences in light waves.