Physics of the mountain car problem

[Rupert Young]

I'm a bit confused by the physics of the mountain car problem.

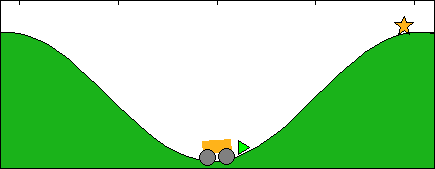
The problem concerns driving an underpowered car up a mountain.

I had expected that the car would be able drive up to a point where the forward force due to acceleration is equal to the opposing force due to gravity and that the car would then just stop.

However, I am finding that the car falls back down and goes up the other slope, and continues to oscillates in that way.

What am I misunderstanding?

Here are the equations.

The landscape curve is given by, cos(3*(x+(pi/2))), where x is the position.

And,
Velocity = Velocity + (Action) * 0.001 + cos(3 * Position) * (-0.0025)
Position = Position + Velocity

where Action = 1
and starting position = -0.5, which is the bottom of the valley.

 

[anorlunda]

Your expectation is wrong. The car's inertia will carry it beyond the point where forces balance, so velocity will go negative and the car will slip back.

I think you are intended to learn that the driver must use both forward and reverse to get enough head start to make it to the top of the hill. It is like rocking a car back and forth to get out of a slippery spot in a snow bank during winter.

 

[nasu]

Your equations do not make much sense, especially the second one which is dimensionally inconsistent.
What do you call "action" in this context? In physics action has a well defined meaning but it doe snot seem this is what you mean here.
There is no force "due to acceleration". The acceleration is due to the net force.
If the car starts with some initial velocity and the engine is shutdown, the only force is gravity and this force will produce the acceleration (opposite to the car's velocity) which will result in the car eventually stopping. Once it stops, the same force will accelerate it down the hill, where is come from. And the process repeats.

 

[A.T.]

What do you call "action" in this context?

https://en.wikipedia.org/wiki/Mountain_Car#Actions

 

[nasu]

Oh, so the car is powered. Thank you for the link.

 

[anorlunda]

The equations in the Wiki article linked are poorly written and poorly documented. But I think the focus is not on accurate physics, but rather on control strategies to achieve a goal, given a set (any set) of equations.