Physics Superposition and Standing Waves (ch. 18)

[Keithkent09]

Homework Statement

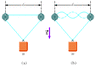
A 6.70 kg object hangs in equilibrium from a string with a total length of L = 5.30 m and a linear mass density of µ = 0.00100 kg/m. The string is wrapped around two light frictionless pulleys that are separated by a distance of d = 2.00 m. (visual is attached) The tension is 41.6 N
At what frequency must the string between the pulleys vibrate in order to form the standing wave pattern shown in (b)? (Visual is attached)

Homework Equations

f=(n/2L)*sqrt(T/u)

The Attempt at a Solution

I already figured out the tension so I plugged in the relevant values and what I thought the value for n might be but nothing I tried worked.

 

[denverdoc]

I get around 150 Hz, is this what you got?

 

[Keithkent09]

The correct answer is 155 and I got 150 one of the times I worked the problem. What did you use for n?

 

[denverdoc]

I used n=3 from the photo. I assume your tension computation was correct. You may want to dbl check to see if it is off a bit.
EDIT seems ok, I get 153hz.

 

[Keithkent09]

Even though the distance over the waves is 2 meters you still set the n to be equal to 3? Are you using the same equation that I used above? The tension is correct that much I do know.

 

[denverdoc]

Even though the distance over the waves is 2 meters you still set the n to be equal to 3? Are you using the same equation that I used above? The tension is correct that much I do know.

Yea, I checked it and get 153Hz. N is the wave number right? So that's what I used as it looks like 1.5 lambda stretched across the 2 meters or am I missing something?

 

[Keithkent09]

Yeah I follow that, what did you do with the 1.5 lambda over two meters though. I thought the n=3 was just inserted straight into the equation.

 

[denverdoc]

Yeah I follow that, what did you do with the 1.5 lambda over two meters though. I thought the n=3 was just inserted straight into the equation.

Which is what I did, just taking the cue for what harmonic from the pic.

 

[ideasrule]

The tension should be 41.27397 N. Using that tension, I got 152.36979 Hz as the final answer.

Note that 150 N, 152 N, 153 N, and 155 N are the same if we ignore the least significant digit.

Don't worry about it; you did it right.

 

[Keithkent09]

When I plug three in for n i get 57.5.
For me the worked out equation looks like this:
f=(3/2L)*(sqrt(41.3/.001)) with L equaling 5.3. What did you do differently?
When I got 150 earlier I had n equaling a much larger value.
Sorry it is taking me so long to get this.

 

[denverdoc]

When I plug three in for n i get 57.5.
For me the worked out equation looks like this:
f=(3/2L)*(sqrt(41.3/.001)) with L equaling 5.3. What did you do differently?
When I got 150 earlier I had n equaling a much larger value.
Sorry it is taking me so long to get this.

I took L=2.0m that is the wave is only present in the top segment and stops at the pullies which I took to be points of forced zero amplitude boundary condition.

 

[Keithkent09]

Oh, I was using L=5.3 instead of just the distance that really mattered as 2. Thank you very much I got the answer now.