Pivoted bar swinging top to bottom

[postfan]

Homework Statement

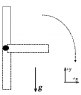
A uniform bar of mass and length is pivoted at one end and is held vertically as shown. After the bar is released, it swings downward with no friction in the pivot.

At the instant the bar is at the bottom of the swing, find the magnitudes of the following quantities:

The angular speed of the bar

The angular acceleration of the bar

The linear speed of the free end of the bar

The horizontal component of the acceleration of the free end of the bar

The vertical component of the acceleration of the free end of the bar

The linear speed of the midpoint of the bar

The horizontal component of the acceleration of the midpoint of the bar

The vertical component of the acceleration of the midpoint of the bar

The horizontal component of the force exerted on the bar by the hinge

The vertical component of the force exerted on the bar by the hinge

Homework Equations

The Attempt at a Solution

For the first part I found the MoI and got 1/3ML^2 through parallel axis, then used conservation of energy : mgh=.5 I w*2 and got sqrt(3*g/L) (used L/2 for h), but it's wrong.

 

[Delphi51]

I got that, too! But I think we have the change in height wrong. The center of mass falls more than L/2; it swings down below the pivot point.

 

[postfan]

Then what is the change in height?

 

[Delphi51]

Initially the center of mass of the swinging bar is L/2 above the pivot.
After the swing it is L/2 below the pivot.
At least that is how it reads to me . . . it actually doesn't say what "at the bottom of the swing" means. The arc shown in the diagram suggests it only goes down to the horizontal orientation. Worth a try to see if a change in height of L produces the "right" answer.

 

[postfan]

You're right. To find the angular acceleration can I use the formula alpha=T/I, and if so does T=Lg?

 

[Delphi51]

T = torque. Yes, that should work. Note that the torque varies with position of the rod as it falls. In fact, the torque appears to be zero initially so I wonder why it falls! Anyway, you will want to sketch a diagram of it in the bottom of the swing position showing the force that causes the torque and its direction so you can see what torque there is.