Place pieces on a chessboard randomly until 2 are adjacent

[fluidistic]

I've written a program that simulates placing pieces randomly on an nxn chessboard, one by one until 2 are adjacent. When 2 are adjacent I stop, and I report the number of pieces it took.
I've plotted a histogram of the number of pieces it took vs number of occurences just to see what kind of distribution it is. To my surprise, with big boards (such as 19x19 like in the game of go), I've noticed a very strange behavior of the histogram/distribution. There is a very slight decrease in probability to stop at 3 pieces compared than to stop at 2 pieces, something that does not happen for smaller boards. I've told this behavior to a friend who studies maths and he didn't trust my results, saying my program is faulty.
So I would like to calculate the exact probability to stop at step 2 and at step 3 for a 19x19 chessboard. I consider that 2 pieces are adjacent when when they are either at the right/left or bottom/top of each other; in diagonal they aren't adjacent.

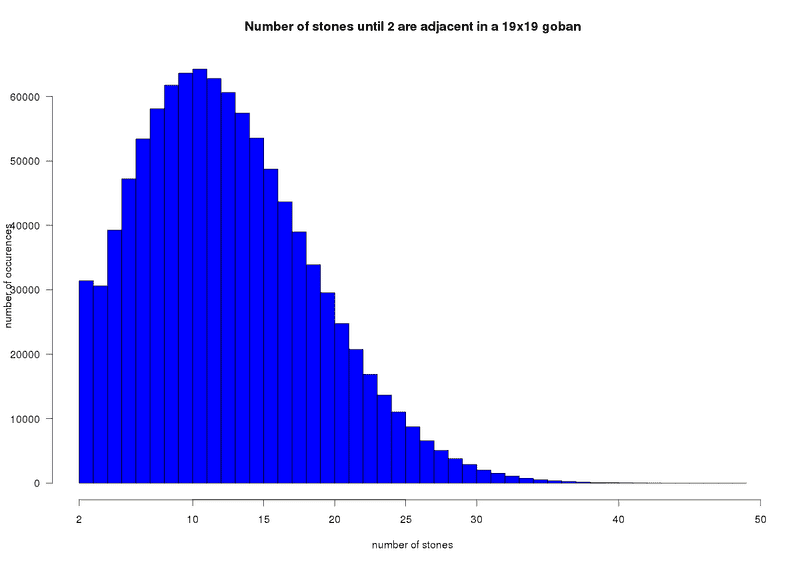
I'd like to have some guidance on how to proceed, I don't really know where to start.

 

[PeroK]

If I understand correctly, the probability of stopping at 2 should be roughly 4/360 and stopping at 3 roughly twice this, about 8/359 times 356/360.

I can't see how it could be more likely to stop at 2 than 3.

 

[PeroK]

Ps from your histogram, what are the relevant probabilities? They both look about 3%.

 

[Merlin3189]

Not an answer to your question (so not posted), but I think I agree with whoever said it doesn't look right.

How often will just two stones be adjacent?
For most squares ther are 4 adjacent squares.
There are 364 squares on the board, so after you place the first stone, there are 364 -1 -4 = 359 squares where you can put the second stone and not be adjacent.
So you expect to get two adjacent two stones adjacent less than 4/359 times. (less than, because for some first squares you have less than 4 adjacent squares.)
Call it 1/90. But you appear to have about 1/30 results for two stones. (Just a rough guess from your graph, as you don't supply raw data. Perhaps a cumulative frequency chart might help.)
For a large number of trials, 1/30 is very different from 1/90.

I haven't got time to do it at the moment, but the exact calculation doesn't look difficult for just two stones, though I can only think, so far, of approximations for higher numbers of stones (unless you do it by brute force on a computer ). My strategy would be to classify squares as having 2,3 or 4 adjacent possible squares, then multiply the fraction of each type by the probability of the next stone being adjacent and sum the results.
So for two, there are 4 squares with 2 adjacent, 68 with 3 adjacent and 292 with 4 adjacent,
then $\frac{4}{364}\times \frac{2}{363} + \frac{68}{364}\times \frac{3}{363} + \frac{292}{364}\times \frac{4}{363}$ = $\frac{4 x 2 + 68 x 3 + 292 x 4}{364 x 363}$ = $\frac{1380}{132132} = 0.0104$

 

[fluidistic]

I'm very sorry guys but it looks like I should have never use a histogram (apparently that's used only for continuous data), but I should have used a barplot. (Someone on IRC just told me that). By doing so, I got a totally different graph and there's no such anomaly:

By the way the occurrences are 10520 and 20891 for 2 and 3 pieces respectively. So problem solved thanks to you guys!
P.S.:If you know the kind of distribution it is (similar to Poisson?), please feel free to say it.

 

[HallsofIvy]

That graph looks like a "Poisson Distribution": https://en.wikipedia.org/wiki/Poisson_distribution.

 

[FactChecker]

It does look like a Poisson distribution, but I don't see any theoretical reason that it should be Poisson. I wonder if a Chi-squared goodness of fit test would say it was Poisson. Just curious.

 

[ChrisVer]

Well, why not a Poisson?
I mean are the different tries dependent to their previous ones?

 

[FactChecker]

Well, why not a Poisson?
I mean are the different tries dependent to their previous ones?

I think the answer is yes. The probabilities change as time goes on (more pieces put on the board).

 

[ChrisVer]

I think the answer is yes. The probabilities change as time goes on (more pieces put on the board).

oh my god, I shoudn't have tried to argue at 5am...
However the diagram is nice...
the 2x2 diagram has pretty much calculable probabilities to fail per turn:
turn 1: 0, you can position your pawn anywhere on the 4 blocks
turn 2: 0.666, you can posiition your pawn anywhere on the 4-1=3 blocs, but 2 of them are marked as "death"... (2/3) to fail, (1/3) to survive
turn 3: 0.333, you had the (1/3) chance to survive from turn 2, and now you have 4-2=2 blocks all of them marked as death. (also using possibilities are complementary)

Can you work the same for a 3x3 diagram?
turn 1: well, the probability to fail is 0, but here things can get "nasty"...because if turn 1 was on an edge (corner or side respectively), there are 2 or 3 blocks respectively marked as "death". that's why I assign to "turn 1" 3 "states", with equal probability 1/N^2= 1/9 (I assume a uniform random distribution) but different multiplicity... the one is the corner (multiplicity = 4), the other is the side (multiplicity=4) and the other is the center (multiplicity=1).
then you expand each of those states to a tree.
I made the trees for this N=3 diagram.

Of course the problem is that the branching of the diagrams is not constant: that is the result of having corners, sides and centers .
At each turn the possibility goes as \frac{\text{multiplicity}}{N^2 - \#\text{turn}}
To obtain the probability at turn k you have to start from the bottom and move to the top ( independent events conditional probability).
So for example in order to reach [starting from the center] to the maximum depth, the probability is:
P(k=6)= 1 \Big|_{\text{turn~6}} \times \frac{1}{5}\Big|_{\text{turn~5}} \times \frac{2}{6}\Big|_{\text{turn~4}} \times \frac{3}{7} \Big|_{\text{turn~3}} \times \frac{4}{8}\Big|_{\text{turn~2}}
if not starting from the center (general to get to depth 6):
P(k=6)= 1 \Big|_{\text{turn~6}} \times \frac{1}{5}\Big|_{\text{turn~5}} \times \frac{2}{6}\Big|_{\text{turn~4}} \times \frac{3}{7} \Big|_{\text{turn~3}} \times \frac{4}{8}\Big|_{\text{turn~2}} \times \frac{1}{9}\Big|_{\text{turn~1}}+ \text{do~same~for~4~that~can~reach~depth~6~of~the~2nd~tree}+\text{same~for~3rd~tree}
But the 3rd tree seems not to contribute.
Another thing you can see is that I got some fixed depth at which the game is over. I suppose it's where your distribution for large turns has to fall to zero.

So things may get worse for larger N, but I'm pretty sure it would be fun to spend some time seeing what happens... eg finding the #turn for the maximum probability vs N?

 

[fluidistic]

My friend calculated the probability to stop at piece 2 and 3 for an nxn sized board (n>6). : P(stop at 2) = 4/(n^2 + n) and P(stop at 3) = (8n^4 - 8n^3 - 52n^2 + 140n - 116)/(n^2 (n^2 - 1) (n^2 - 2)). I think he had to sum up 64 terms or so to get the probability to stop at piece 3. I'm not 100% sure.
He said that for very large boards, stopping at piece 3 is twice more likely than stopping at piece 2 (it tends to the ratio 2:1 for n tends to infinity), because most squares are "middle board squares" (i.e. not corners nor sides).

 

[ChrisVer]

For an NxN board I would say that the pobability to stop at round 2 is:
P(\text{die~at~2}) = P_{\text{survive ~1}} \times P_{\text{hit~next~to~other~at~turn~2}}
If you want to forget about the edges [so take N very large, so that N^2 -(4N-4) \approx N^2] you have that each piece covers 5 boxes [1 that it occupies and 4 over a cross around it].
So the probability to survive turn 1 is P_{\text{survive ~1}}=1 (all board was clear).
And then it would be P_{\text{hit~next~to~other~at~turn~2}}= \frac{4}{N^2-1}...
Because you had N^2 -1 boxes left for that round and 4 cases that achieved the end result.
Again because N^2 \gg 1 you obtain:
P_{\text{die~at~2}} \approx \frac{4}{ N^2}
Similarily to die at turn 3:
P_{\text{die~at~3}}= P_{\text{survive~2}}P_{\text{hit~next~to~other~at~turn~3}} = (1-P_{\text{die~at~2}}) \frac{8}{N^2-2}
P_{\text{die~at~3}} \approx (1 - \frac{4}{N^2} ) \frac{8}{N^2} = 2 \frac{4}{N^2} - \frac{32}{N^4} = 2 P_{\text{die~at~2}} - \mathcal{O}(N^{-4})
So I would agree that with these assumptions you can reach that it reaches a ration 1:2.
In each probability I might be off by a factor of $1/N^2$ from your friend's result because I didn't apply it to the first round; of course it is taken from both 2 and 3, and so their ratio is not influenced by it.

I tried to reproduce your algorithm to make my own checks, but there is something wrong with my checks on the board occupancy. So I can't make those tests, while you can.

 

[fluidistic]

I tried to reproduce your algorithm to make my own checks, but there is something wrong with my checks on the board occupancy. So I can't make those tests, while you can.

Here's my code:

import random
import numpy as np

# Size of the board
n = 19
# Number of trials
trials = 100
# Initialize the board list of lists to 0. 0 means no stone, 1 means stone.
# Note that board[0][0] is the first element and board[20][20] is the last one
# , for when n=19. That's because I define the board
# as n+2 x n+2 for the edges...
board = [[0]*(n+2) for i in range(n+2)]
counter = 0
# Generate random coordinates inside of the 19x19 board
x_coordinates, y_coordinates = random.randint(1, n), random.randint(1, n)

# Now define a boolean function that I'll use as a condition in a while loopdef check_if_stones(x_coordinates, y_coordinates):
  if (board[x_coordinates-1][y_coordinates] == 1
  or board[x_coordinates][y_coordinates-1] == 1
  or board[x_coordinates+1][y_coordinates] == 1
  or board[x_coordinates][y_coordinates+1] == 1):
  return False
  else:
  return True

trial_list = []
for j in range(trials):
  counter = 0
  board = [[0]*(n+2) for i in range(n+2)]
  while check_if_stones(x_coordinates, y_coordinates):
  if board[x_coordinates][y_coordinates] == 0:
  # Now replace a random element by 1
  board[x_coordinates][y_coordinates] = 1
  counter += 1
  x_coordinates, y_coordinates = random.randint(1, n), random.randint(1, n)
  x_coordinates, y_coordinates = random.randint(1, n), random.randint(1, n)
  # Update the counter when the boolean function returns false. Do this outside of the while loop.
  counter += 1
  trial_list.append(counter)
  x_coordinates, y_coordinates = random.randint(1, n), random.randint(1, n)
print('The average number of stones is', np.mean(trial_list))
# print(trial_list)
# print the list into a .txt file
with open('go_data.txt','w') as f:
   f.write(str(trial_list))

I'm not a programmer so this is extremely likely to be a very ugly code but I think it does the job.
Edit: The indentation isn't working well when I paste it here... and that matters a lot to python!

 

[ChrisVer]

Well, to me it's interesting that yours is in python too...maybe it can help debug my code...
Mine is this one... for some reason my checks don't work right

from numpy import zeros
from pylab import show, plot, legend, xlabel, ylabel,text,xlim
import random

#Global variables ,  N variable to create (N-2) x (N-2) board
#                             SUM variable used for normalization

N=5
SUM=0.0

def check(board,x1,y1,x2,y2):
    '''
    checks if positions 1 and position 2 on a board are both filled
    Returns True when both positions are occupied
    Else returns False
    '''
    return board[x1,y1]==1 and board[x2,y2]==1

def end_game(board,pos):
    '''
    Method that takes a board and a new position pos
    Checks adjacent squares to pos and ends the game if necessary
    Returns True when the Filling must stop
    Returns False when the Filling should continue
    '''
    global nTurns
    x,y = pos
    z= check(board,x,y,x+1,y) or check(board,x,y,x-1,y) or check(board,x,y,x,y+1) or check(board,x,y,x,y-1)

    #debugging check inside this if, for N=3 shouldn't get anything
    if nTurns>=6 and z==False:
        print BOARD
        print "x,y=",x,y
        print "x,x+1",check(board,x,y,x+1,y)
        print "x,x-1",check(board,x,y,x-1,y)
        print "y,y+1",check(board,x,y,x,y+1)
        print "y,y-1",check(board,x,y,x,y-1)
        print z
 
    return z

def FillBoard(board):
    '''
    Main Fill method here, takes the Board and
    generates and fills randomly a non-occupied position
    '''
    global BOARD,nTurns

    #Generate position
    xt = random.randrange(1,N-1)
    yt = random.randrange(1,N-1)
    position=xt,yt

    #If occupied retry generating, else fill and change Turn
    if BOARD[xt,yt]==0:
        BOARD[xt,yt]=1
        nTurns+=1
    else:
        FillBoard(BOARD)

    #Recursively move to the next turn until the last position is an end
    if not end_game(BOARD,position):
        FillBoard(BOARD)
def normalize(List):
     '''
    Method that takes a list and normalizes it
    Returns a list of normalized entries
    '''
    m=List
    global SUM
    for element in m:
        SUM+=elelement

    for i in range(len(m)):
        m[i]= 1.*m[i]/sume
 
    return m
'''
MAIN STARTS HERE
'''

L_turns            = []

#Generate 10000 games
for i in range(10000):
    #build an empty board and set the turns to 0 per game started
    BOARD=zeros((N,N),int)
    nTurns=0

    #Start filling the board
    FillBoard(BOARD)

    #At the end of any game put the nTurns to end in list
    L_turns.append(n)

#Create the plotting variables
cL_turns          =list(L_turns)
occurancies    = []
x                      = []

for nTurnsEnd in set(L_turns): #used set because I don't want to count doubles
    x.append(nTurnsEnd)
    occurancies.append(cL_turns.count(nTurnsEnd))
    L_turns.remove(nTurnsEnd)

occurancies= normalize(occurancies)

#Plotting
plot(x,occurancies, 'r*', label=r' N= %g, total events: %g'%(N,SUM))
xlabel('number of turns')
ylabel('normalized occurs')
xlim(0,8)
legend(loc='upper right')
show()