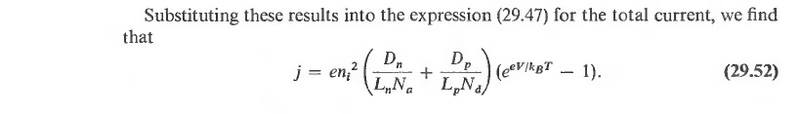Undergrad PN Junction Current: Understanding Dependence on Parameters

[daudaudaudau]

Hi. I'm trying to understand how the current in a PN junction depends on various parameters. I have found this formula in Ashcroft and Mermin. It looks like the current will increase if we decrease the density of donors and/or acceptors, Na and Nd. Is this correct?

 

[mfb]

There is still $n_i^2$.

 

[daudaudaudau]

There is still $n_i^2$.

$n_i^2$ is the intrinsic carrier concentration, which doesn't depend on $N_a$ or $N_d$, so how could that affect the result?

 

[mfb]

Ah wait, you have the doping in the denominators, not the actual number density of electrons/holes. Hmm, then it looks strange.

 

[phyzguy]

The saturation current is caused by the thermal generation of carriers in the depletion region, which are then swept out of the depletion region by the built-in field. As the doping concentration(Na and Nd) goes down, the depletion region gets larger, so there is a larger volume of depleted semiconductor where generation takes place. I think the equation is correct.

 

[daudaudaudau]

The saturation current is caused by the thermal generation of carriers in the depletion region, which are then swept out of the depletion region by the built-in field. As the doping concentration(Na and Nd) goes down, the depletion region gets larger, so there is a larger volume of depleted semiconductor where generation takes place. I think the equation is correct.

Actually this particular derivation in Ashcroft and Mermin doesn't include any generation in the depletion region, but anyway you're right that the formula does make sense when thinking about a reverse biased diode. If we let $p_{no}$ denote the equilibrium density of holes on the N side, and since $n_i^2/N_d=p_{no}$, we can write for the hole current under reverse bias

<br /> J_p=en_i^2\frac{D_p}{L_pN_d}=e\frac{D_p}{L_d}p_{no}<br />

So the reverse hole current is proportional to the density of holes on the N side, which makes sense.

When the diode is forward biased I would like the hole current to depend on the density of holes on the P side. This is of course possible. If $V_{bi}$ is the built-in potential, $V_T$ the thermal voltage, and $p_{po}$ the density of holes on the P side, we have

<br /> p_{no}=p_{po}e^{-V_{bi}/V_T}<br />

Which leads to a hole current that is proportional to $p_{po}=N_a$ and decreases as the built-in potential increases.

<br /> J_p=e\frac{D_p}{L_d}N_ae^{-V_{bi}/V_T}(e^{V/V_T}-1)<br />

So the answer to my initial question must be that the current increases when you decrease $N_a$ because this decreases the built-in potential

<br /> V_{bi}=V_T\log{\frac{N_aN_d}{n_i^2}}<br />

WELL, still puzzling that a low carrier density gives the highest current...