Position of centre of mass in semicircular disc

[gracy]

My teacher taught us how to locate position of centre of mass in semicircular disc
She said circular disc is made up of two semicircles .It's centre of mass is located in centre .But When one of the semicircles is taken out from the circle , only one semicircle is left out.To locate the semicircular's centre of mass she taught us the following method
we will have to take help of calculus or of integration to be more precise .We should choose small semicircular ring of radius "p'and of thickness 'dp'.Total mass of that semicircular disc is given to be "m" and radius "r" so To detect position of centre of mass of semicircular disc we will use following formula
y coordinate of centre of mass=∫mass of that small semicircular ring multiplied by Y coordinate of it's centre of mass/∫dm(mass of that small semicircular ring )
Now mass of the small ring would be equal mass per unit area multiplied by area of ring i.e 2m/π r^2 multiplied by circumference by thickness i.e πp dp.Y coordinate of the ring can be treated as Y coordinate of it's centre of mass .In one of our derivations Y coordinate of semicircular ring came out to be 2 multiplied by it's radius/π
So y coordinate of centre of mass=∫2m/π r^2 multiplied by πp dp ×2pπ/ ∫dm an integration has upper and lower limit of r and zero respectively because we want to take all possible small rings of "0" to "r" radius.
=

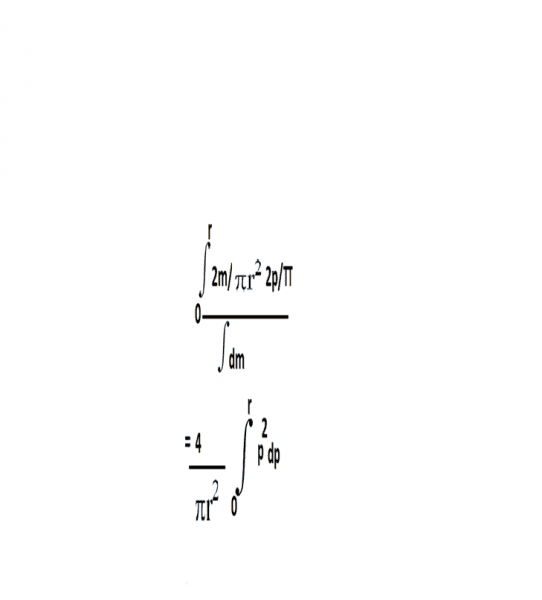
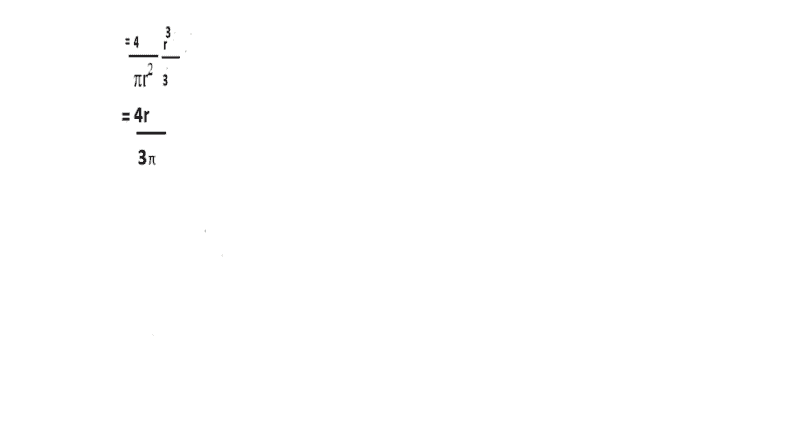
So centre of mass of semicircular disc will be 4r/3 pi vertical distance from origin.I understood all these except how thickness comes out to be dp?How thickness can be derivative of radius(dR)?

 

[Tom_K]

So y coordinate of centre of mass=∫2m/π r^2 multiplied by πp dp ×2pπ/ ∫dm an integration has upper and lower limit of r and zero


So centre of mass of semicircular disc will be 4r/3 pi vertical distance from origin.I understood all these except how thickness comes out to be dp?How thickness can be derivative of radius(dR)?

You perform the operations on the variable inside the integral sign, but the answer emerges in terms of the limits. In this case, p is the dummy variable inside the integral but the limits are in terms of r, so the answer is in term of r.

 

[Delta2]

You confuse the radius of the semicircular disc which is r which is a constant, with the dynamic variable p which represents the position of the infinitesimal circular disc positioned at distance p from the center and spanning the semicircular region between distance p and p+dp. I know it will be hard to understand what i am saying without drawing a diagram or a figure but i believe that's where the problem lies anyway. Did your teacher provide a figure that shows the whole thing. if yes look at it carefully again.

 

[gracy]

In this site also thickness (delta R)is given as derivative of radius(dR)
https://www.math.hmc.edu/funfacts/ffiles/20004.2-3.shtml
In the below lines from the mentioned site
The Math Behind the Fact:
Well, no, it is not a coincidence. For the ball, a small change in radius produces a change in volume of the ball which is equal to the volume of a spherical shell of radius R and thickness (delta R).

 

[Delta2]

Ok let me ask it again, did your teacher provide a diagram or a figure or whatever that shows what exactly he is doing (i.e to show p and dp in the figure) or not?

 

[gracy]

Check this video

from time 11 to 16
although the accent is really hard to understand but it is exactly the same thing which my teacher taught us.I had a hard time understanding the accent but it's the only video I found which has everything I wanted .

to show p and dp in the figure) or not?

Diagram is also in the video given.

 

[Delta2]

Ok the video is good, what is it that u don't understand then? thickness is dp and it shows at the figure why is that. It is like having a rectangle with one side 2πp and the other side dp. Maybe you confused with the semantics of thickness, we don't mean thickness in the z-dimension, but thickness in the radial dimension.

 

[gracy]

But why thickness is dp?

 

[pvk21]

Ok.obviously derivative of radius is thickness of an object.derivative is rate of change of something.let suppose we take a sphere whose radius is r.as radius changed(i.e dr)its thickness eventually increases.we can calculate increased thickness as volume between old radius and new radius.

 

[pvk21]

Well not volume but distance between New radius and old radius

 

[mattt]

Many people don't like those type of "derivations".

From a mathematical point of view, you have the notion of "Integral of a (measurable) function on a (differentiable) manifold" and the "center of mass" of your semi-disk is just a particular case:

$D := (0,R)\times(0,\pi)$ (in polar coordinates) and

$\vec{r}_{CM} :=\frac{\int_D \rho(r,\theta)(x(r,\theta), y(r, \theta) ) |J(r,\theta)| drd\theta}{M}$

if the semi-disk is homogeneous:

$\vec{r}_{CM} :=\frac{\int_D \rho(r,\theta)(x(r,\theta), y(r, \theta) ) |J(r,\theta)| drd\theta}{M} = \frac{\int_0 ^{\pi}\left(\int_0^R\rho (r cos(\theta), r sin(\theta) ) r dr\right)d\theta}{M} =$$=\frac{\rho\int_0 ^{\pi}\left(\int_0^R (r^2 cos(\theta), r^2 sin(\theta) ) dr\right)d\theta}{M} = \frac{\rho\int_0^{\pi}(cos(\theta)[\frac{r^3}{3}]_0^R , sin(\theta) [\frac{r^3}{3}]_0^R ) d\theta}{M}=$$=\frac{\rho R^3 \int_0^{\pi} (cos(\theta), sin(\theta) ) d\theta}{3 M}= \frac{\rho R^3 ( [sin(\theta)]_0^{\pi}, [-cos(\theta)]_0^{\pi})}{3 M}=$$=\frac{\rho R^3}{3 M} (0,2)=\frac{M}{\pi R^2/2}\frac{ R^3}{3 M}(0,2)= \frac{2 R}{3 \pi} (0, 2) = ( 0, \frac{4 R}{3 \pi} )$To be able to undertand the formula

$\vec{r}_{CM} :=\frac{\int_D \rho(r,\theta)(x(r,\theta), y(r, \theta) ) |J(r,\theta)| drd\theta}{M}$

or in general (integral of measurable functions on differentiable manifolds)

you should study Calculus on Manifolds.

 

[pvk21]

dp just indicate that there is only small change in its thickness.change is radius is small that why change in thickness is also small(i.e dp)

 

[Delta2]

But why thickness is dp?

Well the video u post is good , still it doesn't show in a crystal clear way what is p, what is p+dp and the region in between of thickness dp. Maybe someone has to make a figure here but i can't this moment.

 

[pvk21]

dp is change in thickness and p is current thickness.so p+dp must be new thickness of object.

 

[gracy]

dp is change in thickness and p is current thickness.so p+dp must be new thickness of object.

No.p is radius of the ring.

 

[pvk21]

Well ok if p is radius then p+dp will be new radius.