SUMMARY
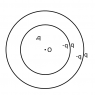
The discussion centers on calculating the electric potential at the center of a non-conducting spherical shell with inner radius R and outer radius 2R, when a point charge q is placed at a distance r from the center. The induced charges on the inner surface of the shell are -q, while the outer surface has +q. The potential at the center is derived from the sum of potentials due to these charge distributions, resulting in the formula kQ(1/r - 1/(2R)). The distinction between conducting and non-conducting shells is crucial for understanding charge distribution and potential calculations.
PREREQUISITES
- Understanding of electrostatics principles
- Familiarity with electric potential and charge distribution
- Knowledge of spherical shells in electrostatics
- Ability to apply Gauss's Law
NEXT STEPS
- Study the concept of electric potential in non-conducting materials
- Learn about the uniqueness theorem in electrostatics
- Explore the implications of charge distribution on spherical shells
- Investigate the differences between conducting and non-conducting shells in electrostatics
USEFUL FOR
Students of physics, particularly those studying electrostatics, electrical engineers, and educators looking to deepen their understanding of charge distribution and electric potential in spherical shells.