- #1
gracy
- 2,486
- 83
External field means field does not belong to or is not of the charges present in it,right?So,if there is a system of two point charges and these charges are present in an external field ,it means this external field is not produced by any of the charges present,right?
Then there is a derivation for Potential energy in an external field
consider two charges ##q_1##, ##q_2## located at ##r_1## and ##r_2## respectively in an external field E. The work done in bringing charge ##q_1##from infinity to r1 is given by ##q_1## V(r1). Similarly, the work done in bringing ##q_2## to ##r_2##, the work done is not only against the external field but also against the field due to ##q_1##.
Work done against the external field = ##q_2## V (r2) and
Work done against the field due to charge ##q_1##
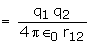
where 'r12' is the distance between charge '##q_1##' and '##q_2##'.
By the superposition principle for field, we add the work done on ##q_2## against the two fields.
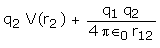
As the path is independent of work, the potential energy of two charges q1, q2 located at r1 and r2 in an external field is given by
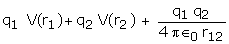 (1`)
(1`)
Here fields of ##q_1##and ##q_2## are negligible.Right?And we have to bring ##q_1##from infinity to ##r_1## first and then ##q_2## from infinity to ##r_2## we just can't pick the two charges together because by doing that we won't get the same expression for Potential energy in an external field as we got in( 1)
Right?
I have underlined my questions!
Then there is a derivation for Potential energy in an external field
consider two charges ##q_1##, ##q_2## located at ##r_1## and ##r_2## respectively in an external field E. The work done in bringing charge ##q_1##from infinity to r1 is given by ##q_1## V(r1). Similarly, the work done in bringing ##q_2## to ##r_2##, the work done is not only against the external field but also against the field due to ##q_1##.
Work done against the external field = ##q_2## V (r2) and
Work done against the field due to charge ##q_1##
where 'r12' is the distance between charge '##q_1##' and '##q_2##'.
By the superposition principle for field, we add the work done on ##q_2## against the two fields.
As the path is independent of work, the potential energy of two charges q1, q2 located at r1 and r2 in an external field is given by
Here fields of ##q_1##and ##q_2## are negligible.Right?And we have to bring ##q_1##from infinity to ##r_1## first and then ##q_2## from infinity to ##r_2## we just can't pick the two charges together because by doing that we won't get the same expression for Potential energy in an external field as we got in( 1)
Right?
I have underlined my questions!