etotheipi
I'm considering the arrangement shown below. Let the positive charge be ##q##, and the negative be ##-q##. To derive the potential energy of this configuration, one usually adds the potential energies of both of the charges in the external field, taking the zero volts equipotential of the external field to be along the line at ##\theta = \frac{\pi}{2}##.
##U = qV_{1} - qV_{2} = q \times -\frac{Ed}{2}\cos{\theta} - q \times \frac{Ed}{2}\cos{\theta} = -E(qd)\cos{\theta} = -\vec{E} \cdot \vec{p}## where ##\vec{p} = q\vec{d}##.
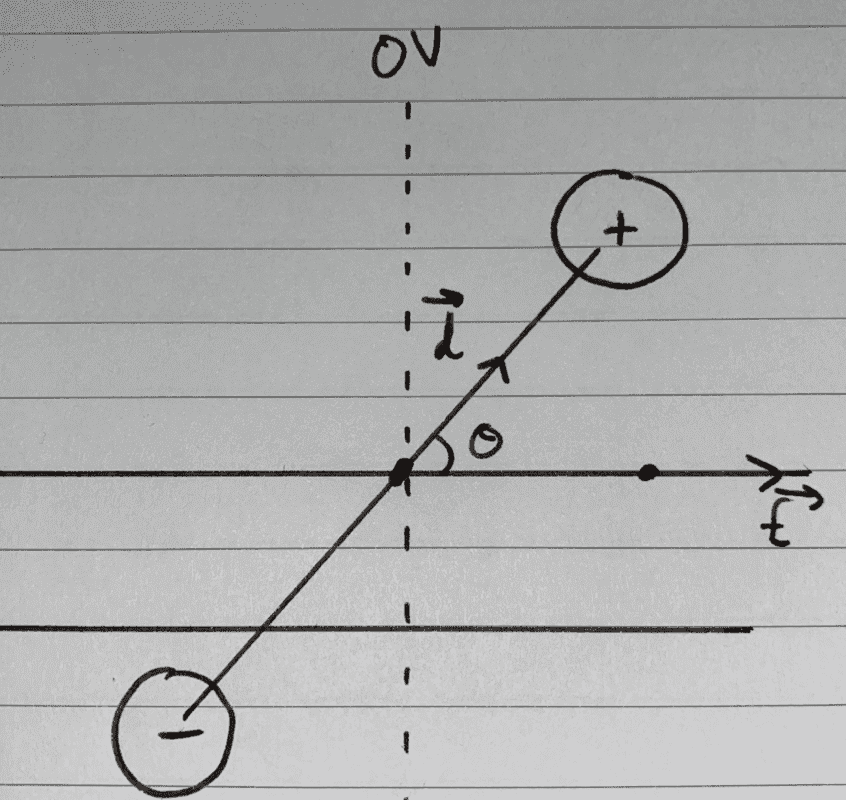
My question is, why isn't the potential energy of the two charges ##U_{3} = -\frac{q^{2}}{4\pi\epsilon_{0}d^{2}}## also included in the summation above?
Since, for any collection of charged particles, the potential energies of subsystems can be added pairwise (i.e. ##-\Delta U = (W_{12} + W_{21}) + (W_{13} + W_{31}) + (W_{23} + W_{32}) = -\Delta U_{a} - \Delta U_{b} - \Delta U_{c}##. And to me, there seem to be three charged things at play here: the source (whatever it happens to be, e.g. perhaps an infinite charged sheet), and the two charges.
Consequently, the potential energy should be the sum of that of the source and +ve charge, the source and -ve charge, and the two charges. Although I think this might be incorrect since I haven't defined ##0V## to be at infinite distance!
##U = qV_{1} - qV_{2} = q \times -\frac{Ed}{2}\cos{\theta} - q \times \frac{Ed}{2}\cos{\theta} = -E(qd)\cos{\theta} = -\vec{E} \cdot \vec{p}## where ##\vec{p} = q\vec{d}##.
My question is, why isn't the potential energy of the two charges ##U_{3} = -\frac{q^{2}}{4\pi\epsilon_{0}d^{2}}## also included in the summation above?
Since, for any collection of charged particles, the potential energies of subsystems can be added pairwise (i.e. ##-\Delta U = (W_{12} + W_{21}) + (W_{13} + W_{31}) + (W_{23} + W_{32}) = -\Delta U_{a} - \Delta U_{b} - \Delta U_{c}##. And to me, there seem to be three charged things at play here: the source (whatever it happens to be, e.g. perhaps an infinite charged sheet), and the two charges.
Consequently, the potential energy should be the sum of that of the source and +ve charge, the source and -ve charge, and the two charges. Although I think this might be incorrect since I haven't defined ##0V## to be at infinite distance!
