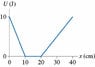
SUMMARY
The discussion focuses on calculating the x-component of force on a particle based on its potential energy graph. The correct formula to use is F = -dU/dx, where the slope of the potential energy graph is constant in the range of 20-40 cm. The participant initially calculated the force at 25 cm as -2 N, which was incorrect due to a misunderstanding of unit conversion and the nature of the slope. The correct approach involves using the average rate of change of potential energy over the interval, confirming that the force remains constant throughout that range.
PREREQUISITES
- Understanding of potential energy and its graphical representation
- Familiarity with calculus concepts, specifically derivatives
- Knowledge of unit conversion, particularly between centimeters and meters
- Basic physics principles regarding force and energy
NEXT STEPS
- Review the concept of derivatives in calculus, focusing on their application in physics
- Study the relationship between potential energy and force in various contexts
- Learn about unit conversions in physics, especially between different measurement systems
- Explore examples of constant force scenarios in physics problems
USEFUL FOR
Students studying physics, particularly those focusing on mechanics and energy concepts, as well as educators looking for clarification on teaching potential energy and force relationships.