TRB8985
- 74
- 15
- Homework Statement
- No homework statement; conceptual question only.
- Relevant Equations
- W = mg
I had a question on the way I've set up my free-body diagrams in the past and was wondering if I've been making mistakes in the setup (despite arriving at the correct answer).
Imagine a very simple situation of stacked blocks, like the the following:
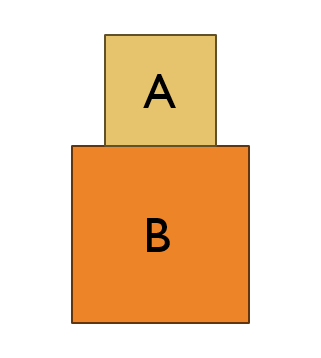
When drawing the free-body diagram of such a situation, previously I was combining the forces of the weights and the normal force acting on B, like this:
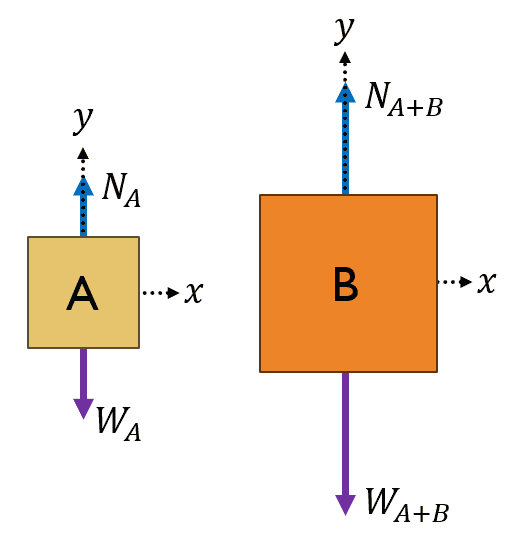
Here's my question: Is this equivalent to the "standard" way of drawing an FBD for this scenario as seen below?
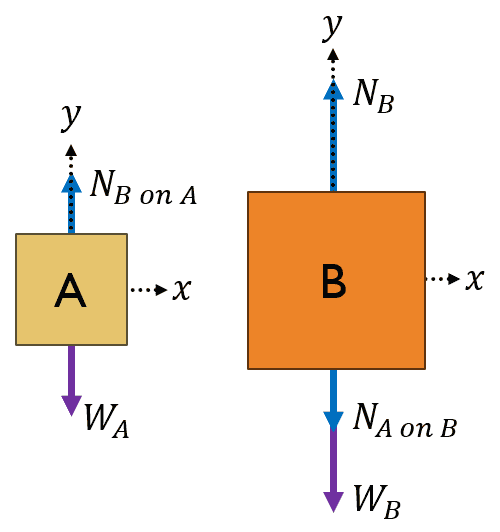
My concern is that, while I was achieving the correct answer, I was being lazy in the setup/notation. Would appreciate any feedback, thanks!
Imagine a very simple situation of stacked blocks, like the the following:
When drawing the free-body diagram of such a situation, previously I was combining the forces of the weights and the normal force acting on B, like this:
Here's my question: Is this equivalent to the "standard" way of drawing an FBD for this scenario as seen below?
My concern is that, while I was achieving the correct answer, I was being lazy in the setup/notation. Would appreciate any feedback, thanks!