yuiop
- 3,962
- 20
I have tried to find a definition of Lie transported vectors on the internet without any luck. (Any help on that would be appreciated). I guess a lot depends on how the congruence is defined. If we have a congruence of members with equal orbital angular velocity, then we have a rigid congruence and members of such a congruence would be at rest with orthonormal basis vectors such that a vector at rest in this congruence that is initially pointing at the centre of the orbit will remain pointing at the centre of the orbit. Rindler is clearly using a rigid congruence to define vorticity and since his equations agree with other sources, it would would appear all definitions of vorticity are relative to a rigid congruence or orthonormal basis vectors. If the formal definition of vorticity is relative to Lie transported vectors and if the formal definition of Lie transported vectors is relative to a congruence of members with equal angular momentum, then things get very messy in the Kerr metric due to sheer. For what its worth I have calculated the averaged rotation of the non rigid equal momentum congruence in the Kerr metric using regular Newtonian fluid dynamics (i.e. the paddle wheel) to be:PeterDonis said:I'm not sure the derivatives you need to take will be well-defined if you restrict to a single ZAMO ring. The physical interpretation of the vorticity requires Lie transported vectors pointing to neighboring members of the congruence; but if you restrict to a single ZAMO ring, there are no "neighboring" members in any direction off the ring, so how can you take the appropriate derivatives in those directions?
##\frac{-4ma(r^2-ma^2/r)}{r^3(r^2+a^2+2ma^2/r)^2}##
This turns out to be a factor of approximately 4/3 larger than the ZAMO precession rate of:
##\frac{-ma(3r^2+a^2)}{r^3(r^2+a^2+2ma^2/r)}##
and approximately 4 times larger than the precession rate of gyroscope held by a static observer in the Kerr metric of:
##\frac{-ma}{r^3(1-2m/r)}##
for large r. I can show how I obtained this result if you are interested. Although this Newtonian fluid vorticity is not exactly equal to the GR precession rate, there does appear to be a close connection.
PeterDonis said:If your response to the above is that we just restrict all derivatives to the two-dimensional subspace of the chosen ZAMO ring, consider that, in order to Einstein synchronize two clocks on the same ZAMO ring, they have to exchange light signals, and those light signals will not be restricted to that ZAMO ring (unless it happens to be at the same radius as a photon orbit). So any physical interpretation of the theorem in question will implicitly have to rely on some extension of the congruence off the chosen ZAMO ring.
The paper referred to by WBN uses "a hollow toroidal tube of glass with perfectly reflecting internal walls" to transit the light signals and so restricts the light path to the ring. Could we not use such a reflecting tube to transmit the synchronisation signals and restrict the analysis to the ring only?
Last edited:

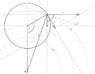
 , is there a physically intuitive way to see why the above integral would necessarily have to vanish, even with ##\omega^a \neq 0##? Do the symmetries of ##\Sigma## (see fig. 1) somehow make the flux of ##\lambda^{-3/2}\omega^{a}## through the Sagnac tube cancel out upon integration?
, is there a physically intuitive way to see why the above integral would necessarily have to vanish, even with ##\omega^a \neq 0##? Do the symmetries of ##\Sigma## (see fig. 1) somehow make the flux of ##\lambda^{-3/2}\omega^{a}## through the Sagnac tube cancel out upon integration?