Pressure difference between the top and bottom surfaces of this cube

AI Thread Summary
The discussion focuses on understanding the pressure difference between the top and bottom surfaces of a cube submerged in a fluid. It clarifies that ρ represents density, not pressure, and that ρl refers to the density of the liquid filling the cube. The pressure within the liquid increases with depth, which is crucial for calculating the pressure difference. The formula discussed relates to the gravitational force acting on the liquid column above the cube. Overall, the pressure difference is influenced by the depth and density of the fluid surrounding the cube.
Say17
Messages
11
Reaction score
1
Homework Statement
We consider the case where the wagon is at rest in profile view (below). Determine the pressure difference deltarho = rho under - delta on between the pressure under the inner surface of the cube and the pressure on the upper surface of the cube.
Relevant Equations
rho = F/A
Hi all,

I think I have to take the formula for pression. rho = F/A -> rho = ma/A but not sure, how to handle it here.

Image 23.06.23 at 17.09.jpeg


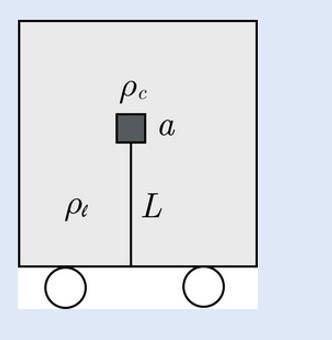
I thought, it should be rho under - rho above = pl*L - pc *a

Solution is: pl *g *a
 
Physics news on Phys.org
ρ stands for density, not pressure. ρl would be the density of the liquid that fills the wagon. (I presume that's what's going on here.)

How does pressure relate to the depth below the surface of a fluid?
 
It's the length from beginning of the cube till ground?
 
The pressure within the liquid depends on the depth below the surface. Pressure increases with depth.

Read this: Static Fluid Pressure
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »
Thread 'Minimum mass of a block'

Thread 'Minimum mass of a block'

Here we know that if block B is going to move up or just be at the verge of moving up ##Mg \sin \theta ## will act downwards and maximum static friction will act downwards ## \mu Mg \cos \theta ## Now what im confused by is how will we know " how quickly" block B reaches its maximum static friction value without any numbers, the suggested solution says that when block A is at its maximum extension, then block B will start to move up but with a certain set of values couldn't block A reach...
View full post »

Similar threads

Pressure of water coming out of a hose nozzle
Replies
7
Views
976
How to calculate the velocity of water streaming into the boat?
Replies
19
Views
974
Buoyancy and the Archimedes Principle
Replies
6
Views
2K
Gauge pressure due to a floating body
Replies
4
Views
2K
Force of water against a dam gate
Replies
29
Views
3K
How do we use Bernoulli's Principle in this situation?
Replies
6
Views
2K
Bouyant force when there is no liquid beneath an object
Replies
8
Views
2K
Calculating Velocity of Water Flow in Open Channel
Replies
11
Views
2K
Misunderstanding of Gravitational Potential Energy
Replies
7
Views
3K
Fluid Mechanics: Head Loss Question (Conceptual)
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top