Pressure measuring device sensitivity

[stunner5000pt]

Homework Statement

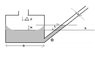
An inclined tube reservoir manometer is constructed as shown in the figure. Analyze the manometer to obtain a general expression for the liquid deflection L in the inclined tube in terms of the applied pressure difference \Delta p. Also obtain a general expression for the manometer sensitivity, and determine the parameter values that gives maximum sensitivity

Homework Equations

The diameter of the large area is D
diameter of the tube is d
H is the difference in heights between the h and H
SGL is the specific gravity of the liquid in question

The Attempt at a Solution

I already solved for L and that expression is used to get the sensitivity
i have no problem getting the sensitivity which is given as
S=\frac{L}{h_{e}}=\frac{1}{SG_{L}\left(\sin\theta+\left(\frac{d}{D}\right)^2\right)}

but they ask to maximize the sensitivity
should i simply differentiate D with respect to theta, D and d and then determine the critical points?

is this enough to maximize sensitivity or i there more i should consider?

thanks for your help

 

[stunner5000pt]

can anyone offer any help or input?

thanks a lot