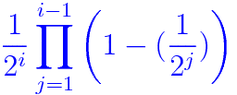bincy
- 38
- 0
Dear friends,
I have divided the time into slots of fixed size. And i toss a coin of probability of heads 1/2 in the first slot. In the next slot, i toss a coin of probability of head 1/4, and in the i^th slot i toss a coin of prob of head 1/2^i. I do this until i get a head. What is the probability distribution of the no. of slots until a success?If it was fixed Prob of heads in each slot, the prob was as easy as a pie. (Geometric)
Initially i thought that, the distribution is View attachment 141for i>=2, and for i=1, prob(i=1)=1/2But this prob distribution do not sum up to one( Mathematica says that it is approximately 0.72). Can anyone explain me why it is not true? What is the real ans?I am perplexed. Thanks in advance.
I have divided the time into slots of fixed size. And i toss a coin of probability of heads 1/2 in the first slot. In the next slot, i toss a coin of probability of head 1/4, and in the i^th slot i toss a coin of prob of head 1/2^i. I do this until i get a head. What is the probability distribution of the no. of slots until a success?If it was fixed Prob of heads in each slot, the prob was as easy as a pie. (Geometric)
Initially i thought that, the distribution is View attachment 141for i>=2, and for i=1, prob(i=1)=1/2But this prob distribution do not sum up to one( Mathematica says that it is approximately 0.72). Can anyone explain me why it is not true? What is the real ans?I am perplexed. Thanks in advance.