Probability of hitting a rotating disc

[Moara]

Homework Statement

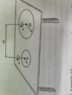
There are two discks rotating with angular velocity w and with radius R and 2R. The distance from there centres is 4R. Find the probability of a particle, that was rotating on the board of the smaller disck, to shock with the bigger after it leaves de disck.

Relevant Equations

V=wr , P(E)=N(E)/U

There are two points of the smaller disck such that a line is tangent to the two discks and passes by that point. If the particle leaves of any point belongin to the arch that connects these two points, then it will hit the other disck. So I managed to calculate the value of this arch and divide it by 2π. But I got the wrong answer. Is this correct ?

 

[BvU]

If your statement is: "it's the wrong answer", then I suppose your statement is correct.

If you don't post what you did, no further help is possible. Show your work ! In detail.

[edit] by the way, is this happening in the vertical plane ? Or did you just rotate the picture to annoy us ?

 

[haruspex]

There are two points of the smaller disck such that a line is tangent to the two discks and passes by that point. If the particle leaves of any point belongin to the arch that connects these two points, then it will hit the other disck.

So far so good, but what value did you calculate for the arc length?

 

[Moara]

If you statement is: "it's the wrong answer", then I suppose your statement is correct.

If you don't post what you did, no further help is possible. Show your work ! In detail.

[edit] by the way, is this happening in the vertical plane ? Or did you just rotate the picture to annoy us ?

Well,

If you statement is: "it's the wrong answer", then I suppose your statement is correct.

If you don't post what you did, no further help is possible. Show your work ! In detail.

[edit] by the way, is this happening in the vertical plane ? Or did you just rotate the picture to annoy us ?

The movement is in the horizontal plane, sorry about the image.

 

[BvU]

I understood that -- I was just being a bit ironic.

Now: both Haru and I are asking you to show your work -- can you do that ?

 

[BvU]

And - as a side note - : it's either disk or disc, but never disck

https://writingexplained.org/disc-or-disk-difference

 

[Moara]

Found my mathematical error while writing my attempt, thank you

 

[BvU]

Often happens -- yet another reason we require posting of a solution attempt

 

[BvU]

Just so you know we take your problems seriously

( I did however use the wrong sign for $\omega$ )

 

[Fred Wright]

I would like to make a further suggestion to the OP. Make a drawing of the system by hand using a compass and ruled straightedge. You can easily look for similar triangles, equal angles and trigonometric relations which are key to solving this problem and quickly check your answer for sanity. Computer drawing programs are nice but the effort in learning to use them can be time consuming and distract from the problem at hand.